C Program to Implement Adjacency Matrix

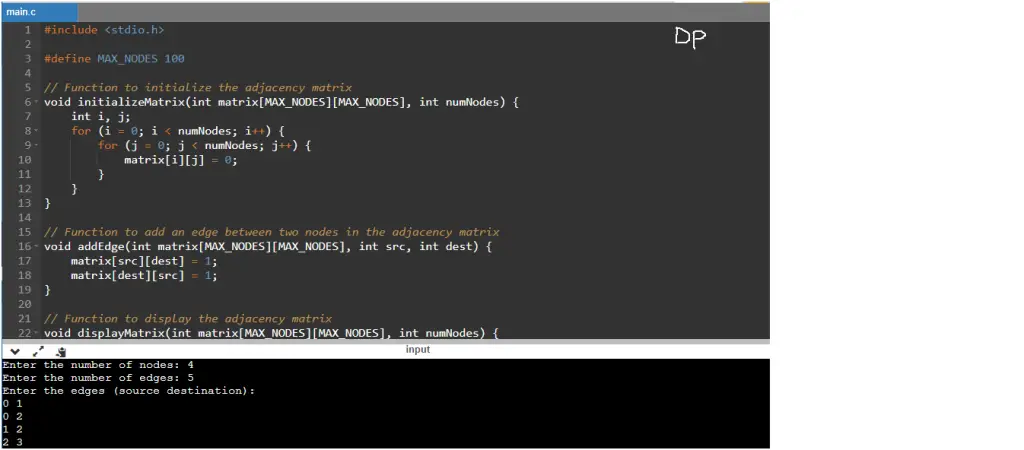
This C program implements an adjacency matrix for a graph. An adjacency matrix is a two-dimensional array where each element (i, j) represents whether there is an edge between vertex i and vertex j in the graph. Typically, the elements are 1 if an edge exists and 0 otherwise.

An adjacency matrix is a common data structure used to represent the connections between nodes in a graph. It is a square matrix where the rows and columns represent the nodes, and the matrix cells indicate whether there is an edge or connection between two nodes.

Program Statement

You are given a graph with ‘n’ nodes and ‘m’ edges. Implement a C program to construct and display the adjacency matrix representation of the given graph.

C Program to Implement Adjacency Matrix

#include <stdio.h>

#define MAX_VERTICES 100

int adjacencyMatrix[MAX_VERTICES][MAX_VERTICES];

void initializeGraph(int numVertices) {
    // Initialize all elements of the adjacency matrix to 0
    for (int i = 0; i < numVertices; i++) {
        for (int j = 0; j < numVertices; j++) {
            adjacencyMatrix[i][j] = 0;
        }
    }
}

void addEdge(int startVertex, int endVertex) {
    // Set the corresponding elements in the adjacency matrix to 1 to represent an edge
    adjacencyMatrix[startVertex][endVertex] = 1;
    adjacencyMatrix[endVertex][startVertex] = 1;
}

void printGraph(int numVertices) {
    printf("Adjacency Matrix:\n");
    
    // Print the adjacency matrix
    for (int i = 0; i < numVertices; i++) {
        for (int j = 0; j < numVertices; j++) {
            printf("%d ", adjacencyMatrix[i][j]);
        }
        printf("\n");
    }
}

int main() {
    int numVertices, numEdges;
    
    printf("Enter the number of vertices: ");
    scanf("%d", &numVertices);
    
    printf("Enter the number of edges: ");
    scanf("%d", &numEdges);
    
    initializeGraph(numVertices);
    
   printf("Enter the edges (start vertex, end vertex):\n");
    for (int i = 0; i < numEdges; i++) {
        int startVertex, endVertex;
        scanf("%d %d", &startVertex, &endVertex);
        addEdge(startVertex, endVertex);
    }
    
    printGraph(numVertices);
    
    return 0;
}

How it works

1. It first prompts the user to enter the number of nodes and edges in the graph.
2. The initializeMatrix function is called to initialize the adjacency matrix. It sets all elements of the matrix to 0, indicating no edges initially.
3. The program asks the user to input the edges by providing the source and destination nodes for each edge. For each edge, the addEdge function is called to update the adjacency matrix.
4. The addEdge function takes the adjacency matrix and the source and destination nodes as parameters. It sets the corresponding cells in the matrix to 1, indicating the presence of an edge between the nodes. Since the graph is undirected, it updates both matrix[src][dest] and matrix[dest][src].
5. After adding all the edges, the program displays the resulting adjacency matrix using the displayMatrix function.
6. The displayMatrix function takes the adjacency matrix and the number of nodes as parameters. It iterates over the matrix and prints the elements, representing the adjacency matrix row by row.

By following these steps, the program constructs the adjacency matrix representation of the given graph and displays it on the screen.

Input/Output