This C program calculates the square root of a given number using the Newton-Raphson method. The Newton-Raphson method is an iterative numerical technique for finding approximations of the roots (in this case, square roots) of a real-valued function.
The square root of a number is a mathematical operation that determines a value which, when multiplied by itself, gives the original number. In programming, finding the square root of a number is a common task that can be accomplished using various algorithms.
Program Statement
Write a C program that calculates the square root of a given number using the Newton-Raphson method. The program should prompt the user to enter a non-negative number and validate the input. It should then calculate the square root with a specified level of precision and display the result.
C Program to Find Square Root of a Number
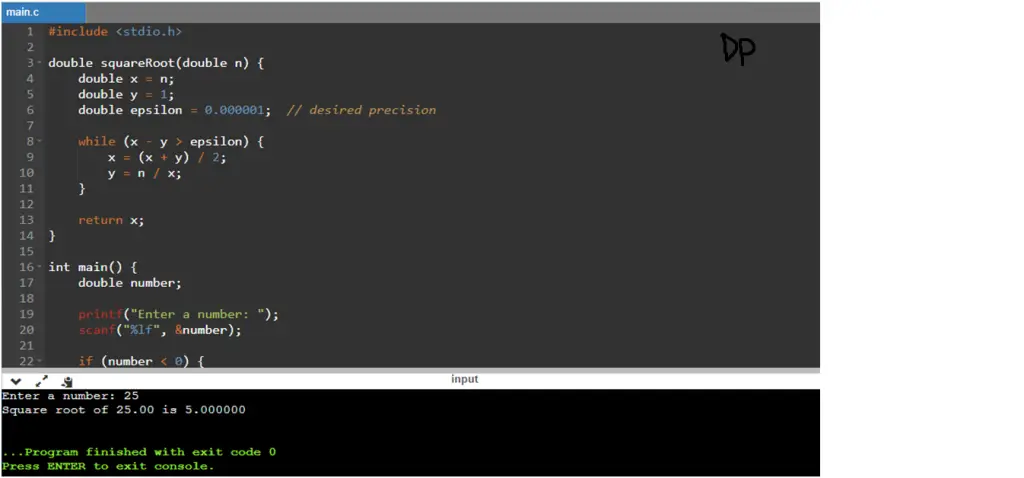
#include <stdio.h>
double squareRoot(double num) {
double epsilon = 0.00001; // Desired precision
double guess = num; // Initial guess
while ((guess * guess - num) > epsilon) {
guess = (guess + num / guess) / 2.0;
}
return guess;
}
int main() {
double number;
printf("Enter a number: ");
scanf("%lf", &number);
double result = squareRoot(number);
printf("Square root of %.2lf is %.4lf\n", number, result);
return 0;
}
How it works
- The program begins by displaying a prompt asking the user to enter a number.
- The input number is read from the user using the
scanffunction and stored in the variablenumber. - The program then validates whether the input number is non-negative. If the number is negative, it displays an error message stating that the square root of a negative number is not defined. The program terminates at this point.
- If the input number is non-negative, the program proceeds to the
squareRootfunction. This function takes the input number as a parameter and calculates its square root using the Newton-Raphson method. - Inside the
squareRootfunction, two variables,xandy, are initialized with the input number and 1, respectively. The variableepsilonis set to a small value, such as 0.000001, to determine the desired precision of the square root calculation. - The function enters a while loop that continues until the difference between
xandyis less than the epsilon value. This ensures that the desired precision is achieved. - In each iteration of the loop,
xis updated as the average ofxandy, andyis updated as the input number divided byx. These steps are based on the Newton-Raphson method, which iteratively refines the guess for the square root. - Once the loop exits, the final value of
xrepresents the calculated square root of the input number. The function returns this value. - Back in the
mainfunction, the calculated square root is stored in the variableresult. - The program then displays the calculated square root with a specified precision using the
printffunction. - Finally, the program terminates, and the execution completes.
The Newton-Raphson method provides a good approximation for the square root of a number, and by iterating the steps, the algorithm refines the guess until the desired precision is achieved.
Input/Output