C# Program to Print Armstrong Number between 1 to 1000

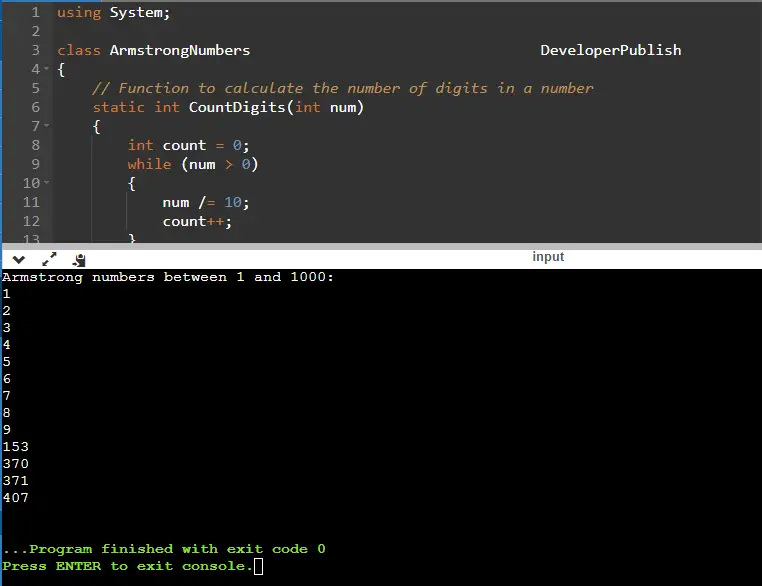
This C# program identifies and prints all Armstrong numbers within the range of 1 to 1000. Armstrong number (also known as a narcissistic number or pluperfect digital invariant) is a number that is equal to the sum of its own digits each raised to the power of the number of digits in the number itself. In other words, an n-digit number is an Armstrong number if the sum of its digits, each raised to the nth power, is equal to the number itself.

Problem Statement

Print Armstrong Numbers between 1 and 1000 using C#

C# Program to Print Armstrong Number between 1 to 1000

using System;

class ArmstrongNumbers
{
    // Function to calculate the number of digits in a number
    static int CountDigits(int num)
    {
        int count = 0;
        while (num > 0)
        {
            num /= 10;
            count++;
        }
        return count;
    }

    // Function to check if a number is an Armstrong number
    static bool IsArmstrong(int num)
    {
        int originalNum = num;
        int numDigits = CountDigits(num);
        int sum = 0;

        while (num > 0)
        {
            int digit = num % 10;
            sum += (int)Math.Pow(digit, numDigits);
            num /= 10;
        }

        return sum == originalNum;
    }

    static void Main()
    {
        Console.WriteLine("Armstrong numbers between 1 and 1000:");

        for (int i = 1; i <= 1000; i++)
        {
            if (IsArmstrong(i))
            {
                Console.WriteLine(i);
            }
        }
    }
}

How it Works

1. CountDigits Function:
   • There’s a helper function called CountDigits that calculates the number of digits in a given number. It’s used to determine the number of digits in each number being checked.
2. IsArmstrong Function:
   • Another helper function called IsArmstrong checks whether a given number is an Armstrong number. It does this by following these steps:
     • It keeps a copy of the original number for later comparison.
     • It calculates the number of digits in the number using the CountDigits function.
     • It initializes a variable to store the sum of the digits raised to the power of the number of digits.
     • It iterates through the digits of the number:
       • Extracts the last digit of the number.
       • Raises the digit to the power of the number of digits.
       • Adds this result to the sum.
       • Removes the last digit from the number.
     • Finally, it compares the calculated sum to the original number. If they are equal, the number is an Armstrong number and the function returns true; otherwise, it returns false.
3. Main Function:
   • The Main function is the entry point of the program.
   • It iterates through numbers from 1 to 1000 using a for loop.
   • For each number in the range, it calls the IsArmstrong function to check if it’s an Armstrong number.
   • If a number is found to be an Armstrong number, it is printed to the console.
4. Printing the Armstrong Numbers:
   • As the program runs, it checks each number in the specified range (1 to 1000) to see if it meets the Armstrong number criteria.
   • When it finds an Armstrong number, it prints it to the console.
5. Final Output:
   • After running the program, you will get a list of Armstrong numbers between 1 and 1000 printed to the console.

Input/ Output