Python Program to Implement Binary Insertion Sort

Binary Insertion Sort is a variation of the traditional Insertion Sort algorithm that utilizes binary search to find the appropriate position for inserting an element into the sorted portion of an array. This modification aims to reduce the number of comparisons required when inserting an element into its correct position within the sorted array.

Problem Statement

You are given an array of integers. Implement the Binary Insertion Sort algorithm in Python to sort the array in ascending order. Your implementation should utilize binary search to find the correct position for inserting each element into the sorted portion of the array.

Python Program to Implement Binary Insertion Sort

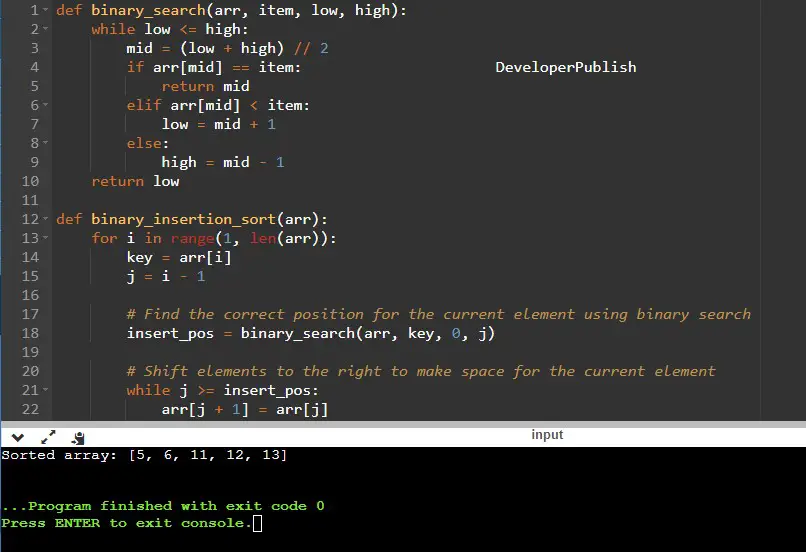
def binary_search(arr, item, low, high):
    while low <= high:
        mid = (low + high) // 2
        if arr[mid] == item:
            return mid
        elif arr[mid] < item:
            low = mid + 1
        else:
            high = mid - 1
    return low

def binary_insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1

        # Find the correct position for the current element using binary search
        insert_pos = binary_search(arr, key, 0, j)

        # Shift elements to the right to make space for the current element
        while j >= insert_pos:
            arr[j + 1] = arr[j]
            j -= 1

        # Insert the current element at the correct position
        arr[insert_pos] = key

# Example usage
arr = [12, 11, 13, 5, 6]
binary_insertion_sort(arr)
print("Sorted array:", arr)

How it Works

1. Initialization: Start with an array of elements where the first element (index 0) is considered as the sorted portion of the array. The rest of the elements (from index 1 to the end) are considered as the unsorted portion.
2. Iterate Through the Unsorted Portion: Begin iterating through the unsorted portion of the array, starting from the second element (index 1).
3. Selecting the Element: For the current iteration, select the element at the current index. This is the element that needs to be inserted into the sorted portion.
4. Binary Search for Insertion Point: Use binary search within the sorted portion of the array to find the correct position (index) where the selected element should be inserted. This involves comparing the selected element with the middle element of the sorted region and adjusting the search range accordingly. The goal is to find the index where the selected element should be placed to maintain the sorted order.
5. Shifting Elements: After finding the insertion point, shift all elements to the right from the insertion point to the end of the sorted portion to create space for the selected element.
6. Insertion: Insert the selected element into the calculated insertion point. This effectively expands the sorted portion of the array.
7. Repeat: Continue these steps for each element in the unsorted portion of the array, gradually expanding the sorted region and ensuring that the elements are sorted at all times.

The key optimization in Binary Insertion Sort is the use of binary search to find the insertion point, which reduces the number of comparisons needed to determine the correct position for each element. However, it’s important to note that even though the number of comparisons is reduced, the shifting of elements can still make Binary Insertion Sort less efficient compared to more advanced sorting algorithms for larger arrays.

In terms of time complexity:

• Each binary search operation takes O(log n) comparisons.
• Shifting elements takes up to O(n) operations in total for all insertions.
• Overall, Binary Insertion Sort has an average and worst-case time complexity of O(n^2), similar to regular Insertion Sort, due to the shifting operations.

While Binary Insertion Sort can be beneficial for small arrays or partially sorted data, more efficient sorting algorithms like Merge Sort or Quick Sort are preferred for larger datasets due to their better average and worst-case time complexity.

Input/ Output