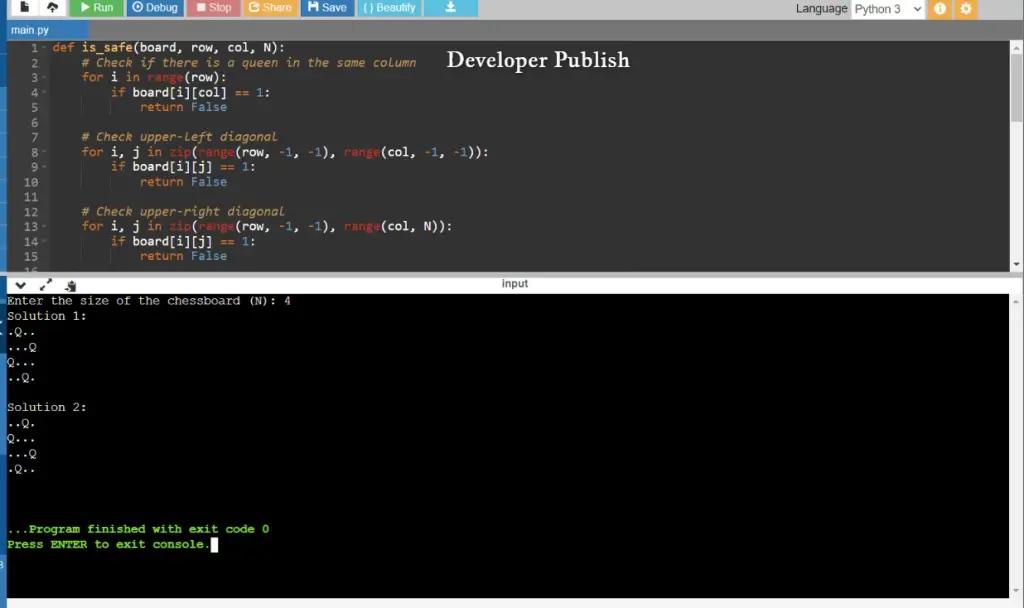
This Python program uses a recursive approach to solve the n-Queens problem. It explores all possible combinations of queen placements on the chessboard while ensuring that queens do not attack each other. The N-Queen problem is a classic puzzle that asks you to place N chess queens on an N×N chessboard so that no two queens threaten each other. In other words, no two queens can share the same row, column, or diagonal.
Problem Statement
Write a Python program to find all possible solutions to the N-Queen problem for a given board size N.
Python Program to Solve n-Queen Problem with Recursion
def is_safe(board, row, col, N):
# Check if there is a queen in the same column
for i in range(row):
if board[i][col] == 1:
return False
# Check upper-left diagonal
for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
if board[i][j] == 1:
return False
# Check upper-right diagonal
for i, j in zip(range(row, -1, -1), range(col, N)):
if board[i][j] == 1:
return False
return True
def solve_n_queens(N):
def solve(board, row):
if row == N:
solutions.append(["".join(["Q" if x == 1 else "." for x in row]) for row in board])
return
for col in range(N):
if is_safe(board, row, col, N):
board[row][col] = 1
solve(board, row + 1)
board[row][col] = 0
solutions = []
chessboard = [[0] * N for _ in range(N)]
solve(chessboard, 0)
return solutions
def print_solutions(solutions):
for i, solution in enumerate(solutions):
print(f"Solution {i + 1}:")
for row in solution:
print(row)
print()
if __name__ == "__main__":
N = int(input("Enter the size of the chessboard (N): "))
solutions = solve_n_queens(N)
print_solutions(solutions)
How it Works
- The
is_safefunction checks whether it is safe to place a queen at a specific position on the chessboard by examining the column and diagonal positions. - The
solve_n_queensfunction uses recursion to find all possible solutions to the N-Queen problem. It initializes an empty chessboard and starts the solving process with the first row. - The
print_solutionsfunction prints all the solutions found.
Input/Output