C# Program to Find Transpose of a Matrix

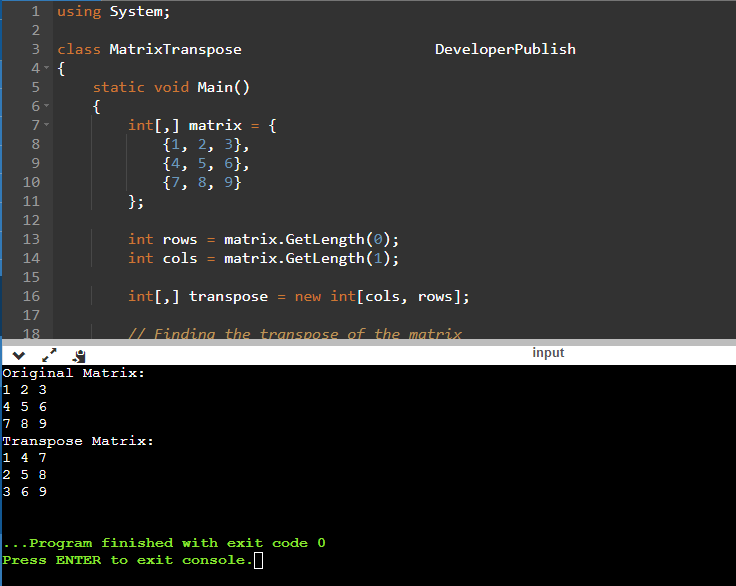
This C# program demonstrates how to calculate the transpose of a matrix. The transpose of a matrix is a new matrix in which the rows of the original matrix become the columns, and the columns become the rows. Transposition is a fundamental operation in linear algebra and matrix manipulation, often used in various scientific and engineering applications.

Problem Statement

Write a C# program to find the transpose of a given matrix. Your program should take an input matrix, perform the transpose operation, and display the resulting transposed matrix.

C# Program to Find Transpose of a Matrix

using System;

class MatrixTranspose
{
    static void Main()
    {
        int[,] matrix = {
            {1, 2, 3},
            {4, 5, 6},
            {7, 8, 9}
        };

        int rows = matrix.GetLength(0);
        int cols = matrix.GetLength(1);

        int[,] transpose = new int[cols, rows];

        // Finding the transpose of the matrix
        for (int i = 0; i < rows; i++)
        {
            for (int j = 0; j < cols; j++)
            {
                transpose[j, i] = matrix[i, j];
            }
        }

        // Displaying the original matrix
        Console.WriteLine("Original Matrix:");
        DisplayMatrix(matrix);

        // Displaying the transpose matrix
        Console.WriteLine("Transpose Matrix:");
        DisplayMatrix(transpose);
    }

    static void DisplayMatrix(int[,] matrix)
    {
        int rows = matrix.GetLength(0);
        int cols = matrix.GetLength(1);

        for (int i = 0; i < rows; i++)
        {
            for (int j = 0; j < cols; j++)
            {
                Console.Write(matrix[i, j] + " ");
            }
            Console.WriteLine();
        }
    }
}

How it Works

1. Original Matrix: Start with the original matrix that you want to transpose. Let’s call this matrix A.
2. Create a New Matrix: Create a new matrix, which will be the transpose of the original matrix. Initialize this new matrix with the appropriate dimensions, which are the reverse of the original matrix’s dimensions. In other words, if the original matrix A is m x n, the new matrix A^T will be n x m.
3. Transpose Elements: Now, go through each element of the original matrix A and copy it to the new matrix A^T, but swap the row and column indices. That is, the element at position (i, j) in matrix A becomes the element at position (j, i) in matrix A^T.You continue this process for all elements in the original matrix, copying them to their corresponding positions in the transposed matrix.
4. Result: After completing the above steps, you’ll have the transposed matrix A^T, where the rows of the original matrix A have become the columns of A^T, and the columns of A have become the rows of A^T.

Input/ Output