C Program to Find Normal and Trace of a Matrix

This C program calculates the normal and trace of a given matrix. It prompts the user to enter the size of the matrix, followed by its elements. It then performs the necessary calculations to find the matrix’s normal (Frobenius norm) and trace, and displays the results.

Problem Statement

Write a C program that reads a matrix of integers from the user and calculates its normal and trace. The program should perform the following steps:

1. Prompt the user to enter the number of rows and columns for the matrix. Make sure the input is within the valid range (1 to 10).
2. Read the elements of the matrix from the user.
3. Display the entered matrix to the user.
4. Calculate the trace of the matrix, if it is a square matrix. The trace is defined as the sum of the elements on the main diagonal (from the top-left to the bottom-right). If the matrix is not square, display a message indicating that the trace cannot be calculated.
5. Calculate the norm of the matrix. The norm of a matrix is defined as the square root of the sum of the squares of its elements.
6. Display the calculated trace and norm to the user.

Ensure that your program handles invalid inputs and provides appropriate error messages when necessary.

Note: You can assume that the maximum size of the matrix is 10×10.

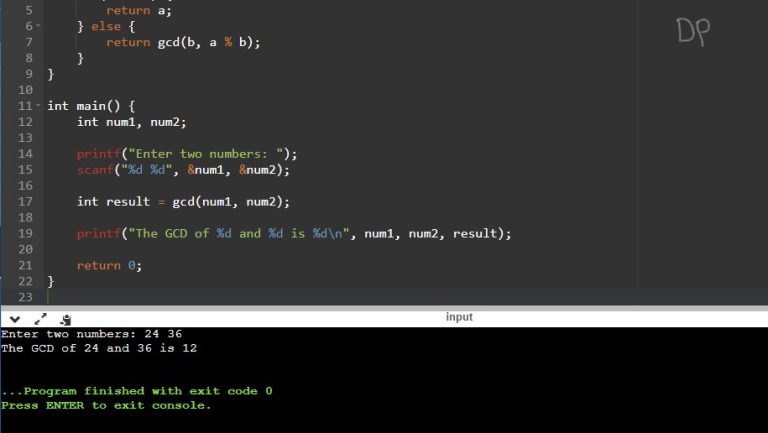
C Program to Find Normal and Trace of a Matrix

#include <stdio.h>

#define MAX_SIZE 10

void readMatrix(int matrix[MAX_SIZE][MAX_SIZE], int rows, int cols) {
    printf("Enter the elements of the matrix:\n");
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            scanf("%d", &matrix[i][j]);
        }
    }
}

void printMatrix(int matrix[MAX_SIZE][MAX_SIZE], int rows, int cols) {
    printf("The matrix is:\n");
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            printf("%d ", matrix[i][j]);
        }
        printf("\n");
    }
}

int calculateTrace(int matrix[MAX_SIZE][MAX_SIZE], int size) {
    int trace = 0;
    for (int i = 0; i < size; i++) {
        trace += matrix[i][i];
    }
    return trace;
}

double calculateNorm(int matrix[MAX_SIZE][MAX_SIZE], int rows, int cols) {
    double norm = 0.0;
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            norm += matrix[i][j] * matrix[i][j];
        }
    }
    norm = sqrt(norm);
    return norm;
}

int main() {
    int matrix[MAX_SIZE][MAX_SIZE];
    int rows, cols;

    printf("Enter the number of rows and columns of the matrix (<= 10):\n");
    scanf("%d%d", &rows, &cols);

    if (rows <= 0 || rows > MAX_SIZE || cols <= 0 || cols > MAX_SIZE) {
        printf("Invalid matrix size.\n");
        return 1;
    }

    readMatrix(matrix, rows, cols);
    printMatrix(matrix, rows, cols);

    if (rows != cols) {
        printf("The matrix is not square. Trace cannot be calculated.\n");
    } else {
        int trace = calculateTrace(matrix, rows);
        printf("The trace of the matrix is: %d\n", trace);
    }

    double norm = calculateNorm(matrix, rows, cols);
    printf("The norm of the matrix is: %lf\n", norm);

    return 0;
}

How it Works?

1. he program starts by prompting the user to enter the number of rows and columns for the matrix. It validates the input to ensure it is within the valid range of 1 to 10.
2. Next, the program reads the elements of the matrix from the user using nested loops. The readMatrix function is responsible for this step.
3. After reading the matrix, the program displays the entered matrix to the user using the printMatrix function. This function uses nested loops to iterate over the matrix elements and prints them in a row-column format.
4. The program then checks if the matrix is square (i.e., the number of rows is equal to the number of columns). If it is square, the program proceeds to calculate the trace of the matrix using the calculateTrace function. This function iterates over the main diagonal elements of the matrix and accumulates their sum.
5. Next, the program calculates the norm of the matrix using the calculateNorm function. This function iterates over all the elements of the matrix, squares each element, and accumulates their sum. The square root of the accumulated sum is then taken to calculate the norm.
6. Finally, the program displays the calculated trace and norm to the user.

Throughout the program, appropriate error messages are displayed if the input is invalid or if the matrix is not square.

Input / Output

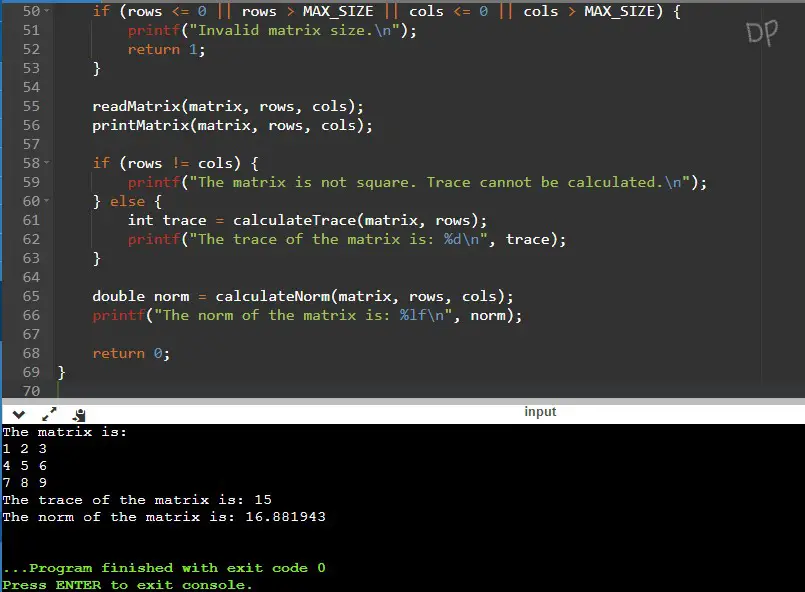
In this example, the user enters a 3×3 matrix with the elements 1 2 3, 4 5 6, and 7 8 9. The program displays the entered matrix and calculates the trace, which is 15, and the norm, which is approximately 16.881943.