Python Program to Find the Sum of Elements in a List using Recursion

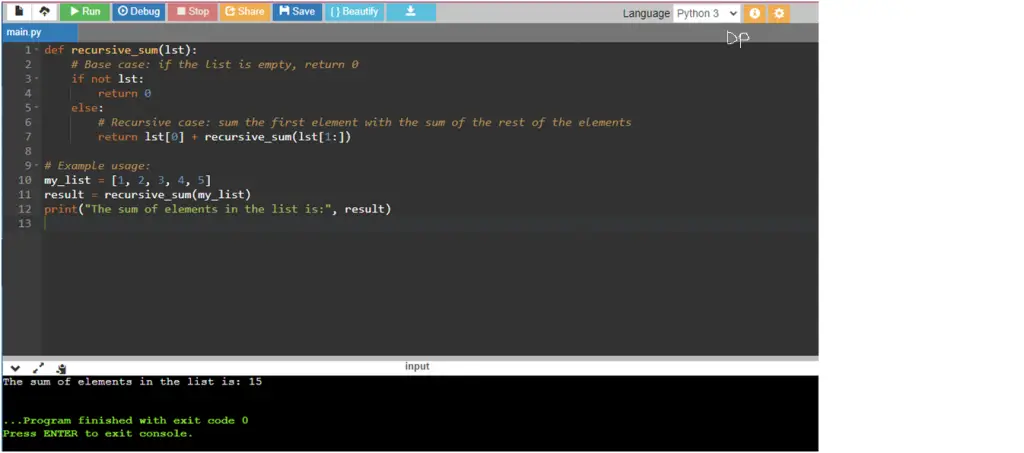
This Python program finds the sum of elements in a list using recursion.

Recursion is a programming technique where a function calls itself in order to solve a problem. To find the sum of elements in a list using recursion, we can break down the problem into smaller parts.

Problem statement

You are given a list of integers. Write a Python program to calculate the sum of all the elements in the list using recursion.

Python Program to Find the Sum of Elements in a List using Recursion

def recursive_sum(lst):
    # Base case: if the list is empty, return 0
    if not lst:
        return 0
    else:
        # Recursive case: sum the first element with the sum of the rest of the elements
        return lst[0] + recursive_sum(lst[1:])

# Example usage:
my_list = [1, 2, 3, 4, 5]
result = recursive_sum(my_list)
print("The sum of elements in the list is:", result)

How it works

To understand how the Python program to find the sum of elements in a list using recursion works, let’s break down the code step by step:

def recursive_sum(lst):
# Base case: if the list is empty, return 0
if not lst:
return 0
else:
# Recursive case: sum the first element with the sum of the rest of the elements
return lst[0] + recursive_sum(lst[1:])

1. Function Definition: We define a function called recursive_sum that takes a single argument, lst, which is the list of integers we want to find the sum of.
2. Base Case: The function starts with a base case check:

if not lst:
return 0

1. If the input list lst is empty (i.e., its length is 0), the function returns 0 immediately. This is the termination condition for the recursion. When we reach an empty list, we know there are no elements left to sum, so we return 0.
2. Recursive Case: If the input list lst is not empty, we enter the else block:

return lst[0] + recursive_sum(lst[1:])

• lst[0] represents the first element of the list. We add this element to the result.
• recursive_sum(lst[1:]) is where the magic of recursion happens. We call the recursive_sum function again with the remaining part of the list, which is all elements except the first one (lst[1:]).

Here’s a visualization of how the program works for the example my_list = [1, 2, 3, 4, 5]:

• First Call: recursive_sum([1, 2, 3, 4, 5]) returns 1 + recursive_sum([2, 3, 4, 5])
• Second Call: recursive_sum([2, 3, 4, 5]) returns 2 + recursive_sum([3, 4, 5])
• Third Call: recursive_sum([3, 4, 5]) returns 3 + recursive_sum([4, 5])
• Fourth Call: recursive_sum([4, 5]) returns 4 + recursive_sum([5])
• Fifth Call: recursive_sum([5]) returns 5 + recursive_sum([])

Now, the base case is reached with an empty list [], so it returns 0.

The results are propagated back up the recursion stack, and the final result is calculated as follows:

1 + (2 + (3 + (4 + (5 + 0))))
1 + (2 + (3 + (4 + 5)))
1 + (2 + (3 + 9))
1 + (2 + 12)
1 + 14
15

So, the sum of elements in the list [1, 2, 3, 4, 5] is indeed 15, as calculated by the recursive function.

Input/Output