Python Program to Find the Length of a List using Recursion

Recursion is a powerful programming concept where a function calls itself to solve a problem. In this Python program, we explore how to calculate the length of a list using recursion. The length of a list is a fundamental piece of information, and understanding how to calculate it recursively is not only a useful coding exercise but also a way to grasp the beauty of recursive algorithms.

Problem statement

You are tasked with writing a Python program that calculates the length of a list using recursion. Your program should take a list as input and return the total number of elements in that list. You must implement this without using any built-in functions or loops.

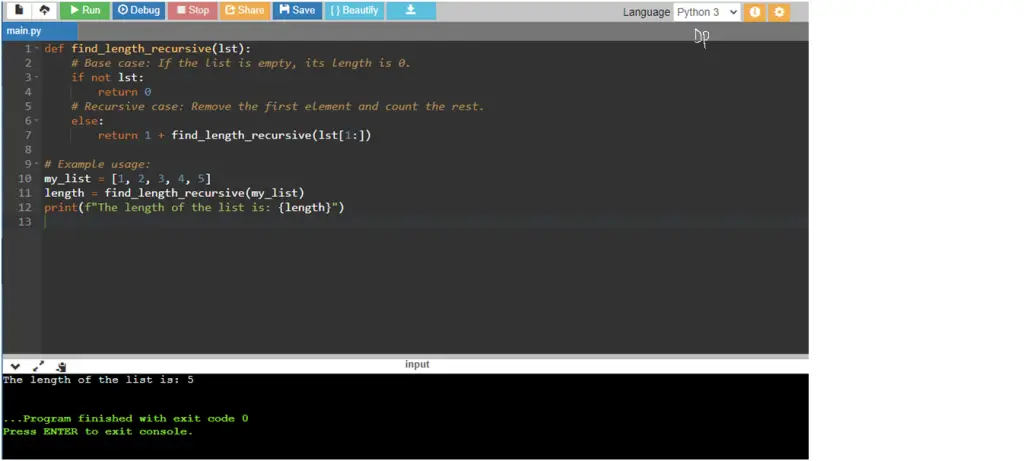
Python Program to Find the Length of a List using Recursion

def find_length_recursive(lst):
    # Base case: If the list is empty, its length is 0.
    if not lst:
        return 0
    # Recursive case: Remove the first element and count the rest.
    else:
        return 1 + find_length_recursive(lst[1:])

# Example usage:
my_list = [1, 2, 3, 4, 5]
length = find_length_recursive(my_list)
print(f"The length of the list is: {length}")

How it works

To understand how the Python program for finding the length of a list using recursion works, let’s break down its functionality step by step:

1. Function Definition: The program defines a function called find_length_recursive that takes a single argument, lst, which is the list for which we want to find the length.
2. Base Case: Inside the find_length_recursive function, there’s a base case check:

if not lst:
return 0

• If the input list lst is empty (i.e., it has no elements), the function returns 0. This is crucial because it serves as the termination condition for our recursion. When the list is empty, we know that its length is 0.

Recursive Case: If the list is not empty, the program enters the else block:

else:
return 1 + find_length_recursive(lst[1:])

• Here, we return 1 plus the result of a recursive call to find_length_recursive with the list lst[1:]. This is the recursive step.
• lst[1:] represents a slice of the list, excluding the first element. So, in each recursive call, we reduce the problem by considering a smaller list without the first element.
• By adding 1 to the result of the recursive call, we are effectively counting the first element in the list.

1. Recursion Unfolding: The recursion continues to unfold until it reaches the base case. In each recursive call, the function chops off one element from the list and adds 1 to the count. This process repeats until the base case is encountered.
2. Backtracking: Once the base case is reached, the recursion starts backtracking. Each recursive call returns its result, and these results are added together as we backtrack through the call stack.
3. Final Result: The final result is the sum of all the 1s added at each step in the recursion, effectively counting all the elements in the list.
4. Example Usage: The program demonstrates the find_length_recursive function by calling it with an example list:

my_list = [1, 2, 3, 4, 5]
length = find_length_recursive(my_list)
print(f”The length of the list is: {length}”)

• In this example, the program calculates and prints the length of my_list.

Overall, this recursive approach to finding the length of a list is elegant and demonstrates how recursion can be used to solve problems by breaking them down into smaller, simpler subproblems. Each recursive call handles a part of the list, and the results are combined to give the final answer.

Input/Output