Python Program to Implement Insertion Sort

Insertion Sort is a simple and intuitive sorting algorithm that builds the final sorted array one item at a time. It’s a comparison-based sorting technique that is particularly useful for small arrays or partially sorted arrays. The algorithm works by maintaining a “sorted” portion of the array and repeatedly inserting elements from the unsorted portion into the correct position within the sorted portion.

Problem Statement

You are given an array of integers. Your task is to implement the Insertion Sort algorithm in python to sort the array in non-decreasing order.

Python Program to Implement Insertion Sort

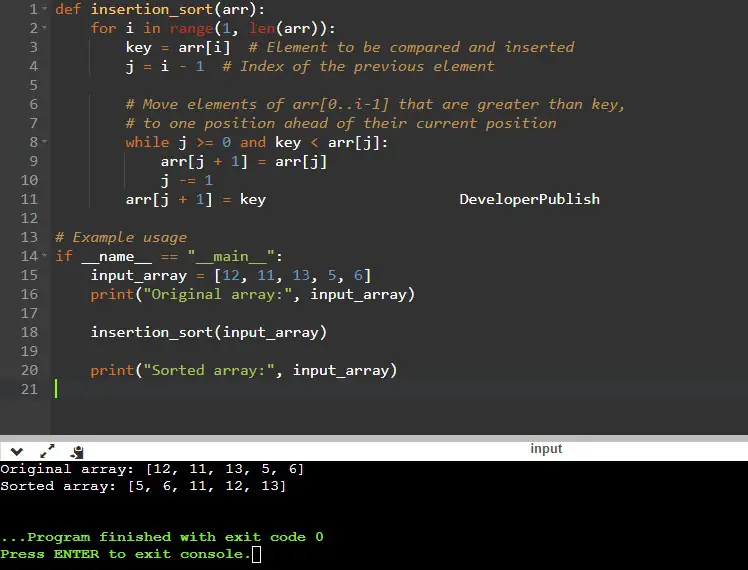
def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]  # Element to be compared and inserted
        j = i - 1  # Index of the previous element

        # Move elements of arr[0..i-1] that are greater than key,
        # to one position ahead of their current position
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key

# Example usage
if __name__ == "__main__":
    input_array = [12, 11, 13, 5, 6]
    print("Original array:", input_array)
    
    insertion_sort(input_array)
    
    print("Sorted array:", input_array)

How it Works

1. Initial State: The first element of the array is considered as a sorted subarray of size 1. This is because a single element is inherently sorted.
2. Iterative Process: Starting from the second element (index 1), the algorithm iterates through the unsorted portion of the array, considering one element at a time.
3. Comparison and Insertion: For each element in the unsorted portion, the algorithm compares it with the elements in the sorted portion (left side) of the array. It repeatedly shifts larger elements to the right until it finds the correct position for the current element.
4. Insertion: Once the correct position is found, the current element is inserted into the sorted portion of the array at that position. This involves shifting the elements as necessary to make space for the insertion.
5. Repeat: Steps 3 and 4 are repeated for each remaining element in the unsorted portion until all elements are processed. This gradually expands the sorted portion of the array.

Here’s a step-by-step breakdown of how Insertion Sort works using the array [12, 11, 13, 5, 6]:

1. Pass 1:
   • Consider the second element, 11.
   • Compare 11 with the element in the sorted portion, 12. Since 11 is smaller, shift 12 one position to the right.
   • Insert 11 in the vacated position.
   • Array after Pass 1: [11, 12, 13, 5, 6]
2. Pass 2:
   • Consider the third element, 13.
   • Compare 13 with 12. Since 13 is larger, leave 12 in place.
   • Insert 13 after 12.
   • Array after Pass 2: [11, 12, 13, 5, 6]
3. Pass 3:
   • Consider the fourth element, 5.
   • Compare 5 with 13 and move 13 one position to the right.
   • Compare 5 with 12 and move 12 one position to the right.
   • Compare 5 with 11 and move 11 one position to the right.
   • Insert 5 in the vacated position.
   • Array after Pass 3: [5, 11, 12, 13, 6]
4. Pass 4:
   • Consider the fifth element, 6.
   • Compare 6 with 13 and move 13 one position to the right.
   • Compare 6 with 12 and move 12 one position to the right.
   • Compare 6 with 11 and move 11 one position to the right.
   • Compare 6 with 5 and insert 6 after 5.
   • Array after Pass 4: [5, 6, 11, 12, 13]

After all passes are completed, the array is fully sorted.

Insertion Sort builds the sorted array gradually by placing each element in its correct position. However, due to its nested loop structure, it has a time complexity of O(n^2) for average and worst cases, where n is the number of elements in the array. This makes it less efficient than some other sorting algorithms for larger arrays.

Input/ Output