Python Program to Check Prime Number

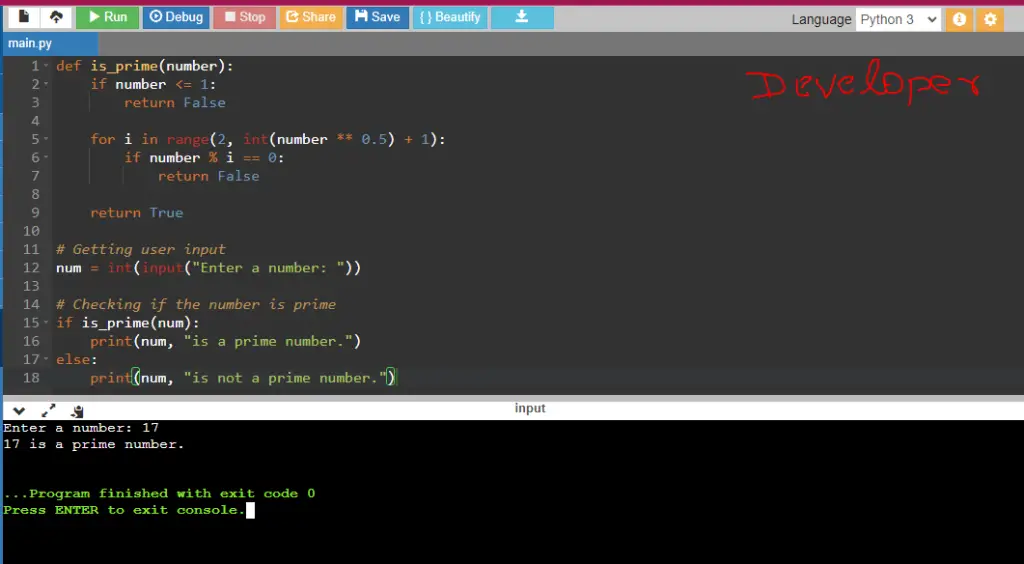
In this Python program, we will check whether a given number is prime or not. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.

Problem statement

Given a number, we need to determine whether it is a prime number or not.

Python Program to Check Prime Number

def is_prime(number):
    if number <= 1:
        return False

    for i in range(2, int(number ** 0.5) + 1):
        if number % i == 0:
            return False

    return True

# Getting user input
num = int(input("Enter a number: "))

# Checking if the number is prime
if is_prime(num):
    print(num, "is a prime number.")
else:
    print(num, "is not a prime number.")

How it works

1. We define a function is_prime(number) to check whether the given number is prime or not.
2. If the number is less than or equal to 1, it is not prime, so we return False.
3. We iterate from 2 to the square root of the given number (using int(number ** 0.5) + 1) and check if the number is divisible by any of the values in this range.
4. If the number is divisible by any value, it is not prime, so we return False.
5. If the number is not divisible by any value, it is prime, so we return True.
6. In the main program, we get user input for the number to be checked.
7. We call the is_prime() function with the user-provided number and check the returned value.
8. Finally, we print whether the number is prime or not based on the returned value.

Input / Output