C Program to Print Armstrong Number between 1 to 100

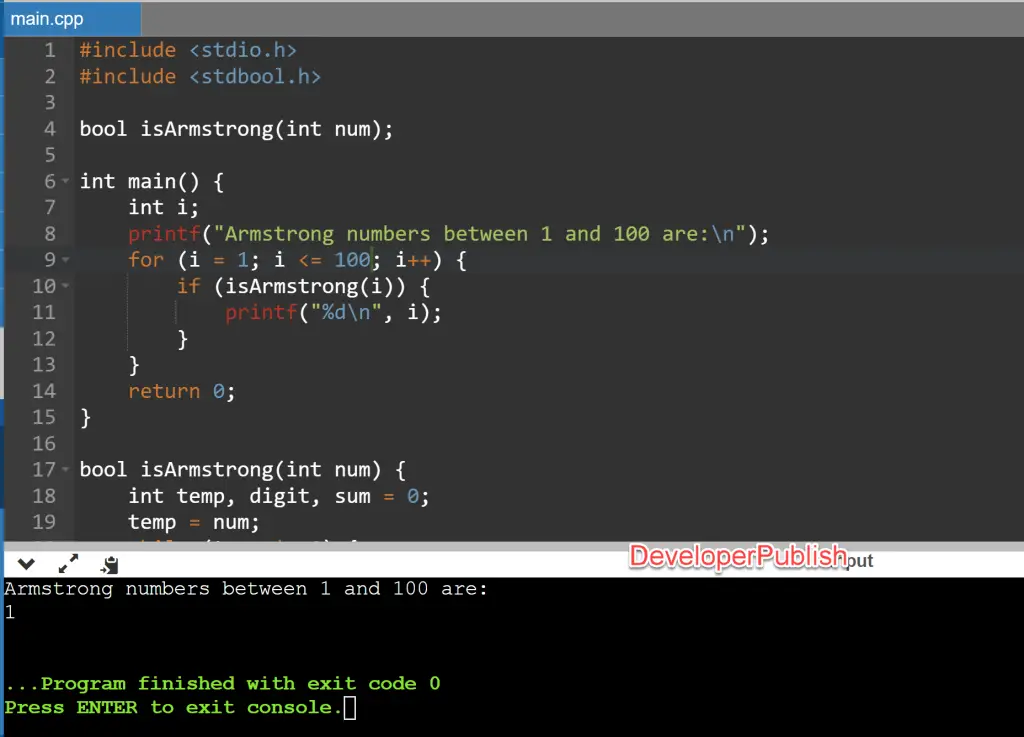
This program prints all Armstrong numbers between 1 and 100 in the C programming language.

Problem Statement

Given a range of natural numbers from 1 to 100, write a C program to find and print all Armstrong numbers in this range.

Solution

To solve this problem, we will write a function called isArmstrong() that takes an integer argument num and returns a boolean value indicating whether or not num is an Armstrong number. We will then use a loop to iterate over all numbers from 1 to 100 and print those that are Armstrong numbers. Here’s the code:

#include <stdio.h>
#include <stdbool.h> 

bool isArmstrong(int num);

int main() {
    int i;
    printf("Armstrong numbers between 1 and 100 are:\n");
    for (i = 1; i <= 100; i++) {
        if (isArmstrong(i)) {
            printf("%d\n", i);
        }
    }
    return 0;
}

bool isArmstrong(int num) {
    int temp, digit, sum = 0;
    temp = num;
    while (temp != 0) {
        digit = temp % 10;
        sum += digit * digit * digit;
        temp /= 10;
    }
    return num == sum;
}

Output

Let’s go through the code step-by-step:

1. We include the standard input/output header file stdio.h and the boolean header file stdbool.h.
2. We declare a function called isArmstrong() that takes an integer argument num and returns a boolean value. This function will be used to check if a number is an Armstrong number or not.
3. In the main() function, we declare an integer variable i and use a loop to iterate over all numbers from 1 to 100. For each number, we call the isArmstrong() function to check if it is an Armstrong number. If it is, we print it using the printf() function.
4. The isArmstrong() function is defined below the main() function. It takes a single integer argument num, which is the number to be checked for Armstrong property.
5. Inside the isArmstrong() function, we declare three integer variables temp, digit, and sum. We initialize temp to num, which will be used to extract each digit of num. We initialize sum to 0, which will be used to store the sum of cubes of digits of num.
6. We then use a while loop to extract each digit of num and add its cube to sum. We divide temp by 10 to remove the last digit of num. This process continues until temp becomes 0.
7. Finally, we check if num is equal to sum. If it is, we return true (indicating that num is an Armstrong number), otherwise we return false.

Explanation

An Armstrong number is a number that is equal to the sum of cubes of its digits. For example, 153 is an Armstrong number because 1^3 + 5^3 + 3^3 = 153. To check if a number is an Armstrong number, we need to extract each digit of the number, cube it, and add the cubes. If the result is equal to the original number, then the number is an Armstrong number.

The isArmstrong() function takes an integer argument num and extracts each digit of num using a while loop. Inside the loop, we extract the last digit of num using the modulus operator % and store it in the variable digit. We then cube digit and add it to sum. We remove the last digit of num by dividing temp by 10, and the loop continues until temp becomes 0. Once the loop is finished, we check if num is equal to sum. If it is, we return true, indicating that num is an Armstrong number. If it isn’t, we return false.

In the main() function, we use a loop to iterate over all numbers from 1 to 100. For each number, we call the isArmstrong() function to check if it is an Armstrong number. If it is, we print it using the printf() function.

Conclusion

In this program, we used a loop and a function to find all Armstrong numbers between 1 and 100 in the C programming language. Armstrong numbers are numbers that are equal to the sum of cubes of their digits. By extracting each digit of a number, cubing it, and adding the cubes, we can check if a number is an Armstrong number. The isArmstrong() function uses this process to check if a number is an Armstrong number, and the main() function uses a loop to find and print all Armstrong numbers between 1 and 100.