C Program to Find Sum of Natural Numbers using Recursion

This program calculates the sum of the first n natural numbers using recursion in the C programming language.

Problem Statement

Given a positive integer n, write a C program to calculate the sum of the first n natural numbers using recursion.

Solution

To solve this problem, we will write a function called sum() that takes an integer argument n and recursively calculates the sum of the first n natural numbers. Here’s the code:

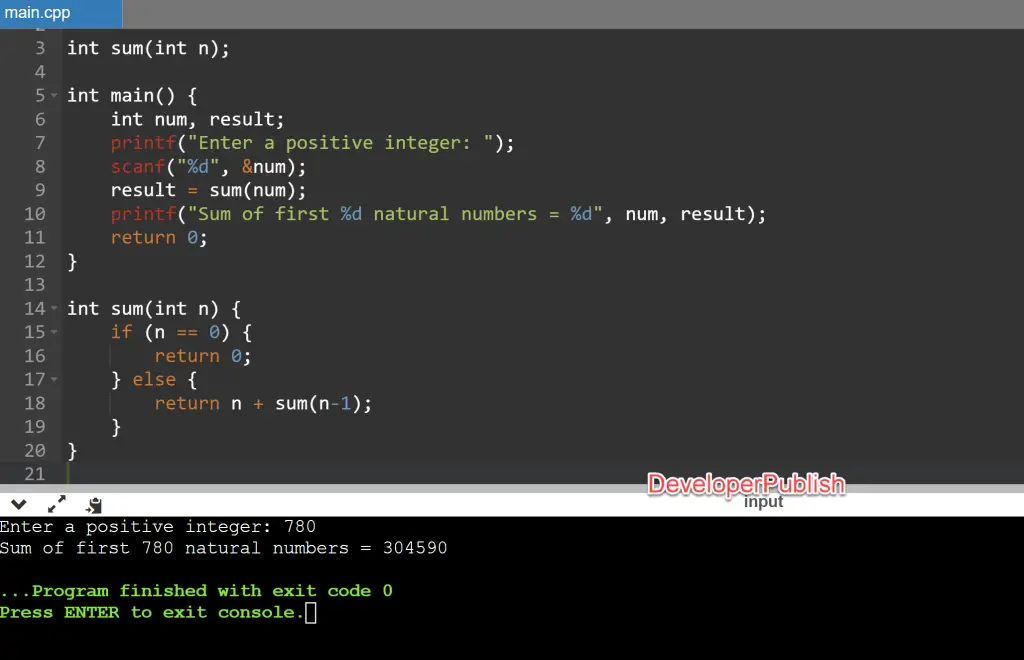
#include <stdio.h>

int sum(int n);

int main() {
    int num, result;
    printf("Enter a positive integer: ");
    scanf("%d", &num);
    result = sum(num);
    printf("Sum of first %d natural numbers = %d", num, result);
    return 0;
}

int sum(int n) {
    if (n == 0) {
        return 0;
    } else {
        return n + sum(n-1);
    }
}

Output

Let’s go through the code step-by-step:

1. We include the standard input/output header file stdio.h.
2. We declare a function called sum() that takes an integer argument n and returns an integer value. This function will be used to recursively calculate the sum of the first n natural numbers.
3. In the main() function, we declare two integer variables num and result. We prompt the user to enter a positive integer using the printf() and scanf() functions. We then call the sum() function with the input num as an argument and store the result in the result variable.
4. Finally, we use the printf() function to display the result to the user.
5. The sum() function is defined below the main() function. It takes a single integer argument n, which is the number of natural numbers to be summed up.
6. If the input n is 0, the function returns 0 (the base case).
7. Otherwise, the function returns the sum of n and the result of calling sum(n-1) (the recursive case). This recursive call reduces the value of n by 1 each time until the base case is reached.
8. This process continues until n is reduced to 0.

Explanation

The sum() function is the core of the program. It calculates the sum of the first n natural numbers by using recursion. Recursion is a programming technique where a function calls itself to solve a smaller version of the same problem. The sum() function follows this technique to calculate the sum of the first n natural numbers.

The function sum() has two cases: the base case and the recursive case. The base case is where the function terminates and returns a value. In this case, if the input n is 0, the function returns 0. The recursive case is where the function calls itself to solve a smaller version of the same problem. In this case, if the input n is greater than 0, the function returns the sum of n and the result of calling sum(n-1).

When the sum() function is called with an input value of n, it calculates the sum of the first n natural numbers by recursively calling itself with a smaller value of n. This process continues until the base case is reached (i.e., n becomes 0). At that point, the function starts returning values to its previous calls. The values

returned by the function are added up until the original call to sum() is reached, which returns the final sum of the first n natural numbers.

In the main() function, we prompt the user to enter a positive integer num. We then call the sum() function with the input num as an argument and store the result in the result variable. Finally, we use the printf() function to display the result to the user.

Conclusion

In this program, we used recursion to calculate the sum of the first n natural numbers in the C programming language. Recursion is a powerful technique that can be used to solve a wide variety of problems. The key to writing a good recursive function is to identify the base case and the recursive case. The base case is the case where the function terminates and returns a value. The recursive case is the case where the function calls itself to solve a smaller version of the same problem. By combining these two cases, we can write powerful and elegant recursive functions that solve complex problems with ease.