Python Program to Implement Ternary Heap

This Python program implements a ternary heap, which is a type of min-heap where each parent node has up to three child nodes.

A Ternary Heap is a variant of a binary heap, a fundamental data structure used in computer science for implementing priority queues. While a binary heap organizes its elements in a binary tree structure where each node has at most two children (left and right), a ternary heap allows each node to have up to three children. This variation can sometimes offer performance advantages in certain scenarios.

Problem Statement

Design and implement a Ternary Heap data structure in python.

Python Program to Implement Ternary Heap

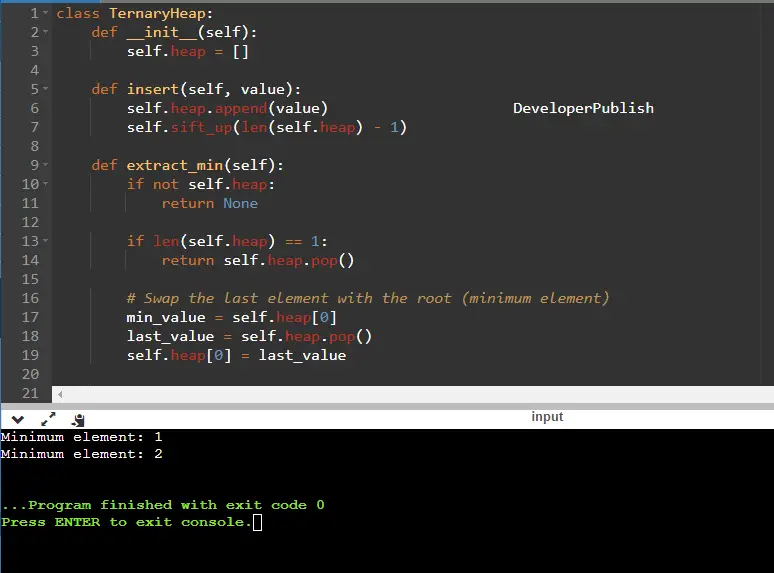
class TernaryHeap:
    def __init__(self):
        self.heap = []

    def insert(self, value):
        self.heap.append(value)
        self.sift_up(len(self.heap) - 1)

    def extract_min(self):
        if not self.heap:
            return None

        if len(self.heap) == 1:
            return self.heap.pop()

        # Swap the last element with the root (minimum element)
        min_value = self.heap[0]
        last_value = self.heap.pop()
        self.heap[0] = last_value

        # Sift down to maintain the heap property
        self.sift_down(0)

        return min_value

    def sift_up(self, index):
        while index > 0:
            parent_index = (index - 1) // 3
            if self.heap[index] < self.heap[parent_index]:
                self.heap[index], self.heap[parent_index] = self.heap[parent_index], self.heap[index]
                index = parent_index
            else:
                break

    def sift_down(self, index):
        while True:
            left_child_index = 3 * index + 1
            middle_child_index = 3 * index + 2
            right_child_index = 3 * index + 3
            smallest = index

            if (
                left_child_index < len(self.heap)
                and self.heap[left_child_index] < self.heap[smallest]
            ):
                smallest = left_child_index

            if (
                middle_child_index < len(self.heap)
                and self.heap[middle_child_index] < self.heap[smallest]
            ):
                smallest = middle_child_index

            if (
                right_child_index < len(self.heap)
                and self.heap[right_child_index] < self.heap[smallest]
            ):
                smallest = right_child_index

            if smallest != index:
                self.heap[index], self.heap[smallest] = self.heap[smallest], self.heap[index]
                index = smallest
            else:
                break

    def peek_min(self):
        if not self.heap:
            return None
        return self.heap[0]

    def is_empty(self):
        return len(self.heap) == 0

    def size(self):
        return len(self.heap)

# Example usage:
heap = TernaryHeap()
heap.insert(5)
heap.insert(2)
heap.insert(9)
heap.insert(1)
heap.insert(6)

print("Minimum element:", heap.extract_min())  # Output: Minimum element: 1
print("Minimum element:", heap.extract_min())  # Output: Minimum element: 2

How it Works

1. Insertion:

• When you insert a new element into a Ternary Heap, you add it as a leaf node at the leftmost available position in the last level of the tree.
• After inserting the element, you may need to ensure that the heap property is maintained. To do this, you perform a “sift-up” operation:
  • Compare the newly inserted element with its parent (the parent is the node at index (i-1)//3 if the new element is at index i).
  • If the newly inserted element is smaller (for a min-heap) than its parent, swap them.
  • Repeat this process until the element is in its correct position, or until you reach the root of the heap.

2. Extraction (Extracting the Minimum Element):

• To extract the minimum element from a min-heap (or maximum from a max-heap), you typically take the element at the root, which is guaranteed to be the smallest (or largest) element in the heap.
• After removing the root, you need to ensure that the heap property is preserved. To do this, you perform a “sift-down” operation:
  • Replace the root with the last leaf node in the heap.
  • Compare this new root with its children (up to three children in a ternary heap).
  • Swap the root with the smallest child if it is larger than that child (for a min-heap). Repeat this process until the heap property is satisfied for all nodes.

3. Peek (Viewing the Minimum Element):

• To peek at the minimum element (or maximum for a max-heap) without removing it, you simply look at the root of the heap. This operation has a time complexity of O(1) because you don’t need to perform any swaps or adjustments.

4. Is Empty:

• To check if the Ternary Heap is empty, you can simply check if the underlying array or list is empty.

5. Size:

• To determine the number of elements in the Ternary Heap, you can count the elements in the underlying array or list.

Input/ Output