Python Program to Check if Undirected Graph is Bipartite using BFS

This Python program checks if an undirected graph is bipartite using BFS and a color-coding approach. A bipartite graph can be divided into two sets of vertices such that no two vertices within the same set are connected by an edge.

In graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets such that no two vertices within the same set are adjacent. We can use the Breadth-First Search (BFS) algorithm to check if an undirected graph is bipartite.

Problem Statement

Write a Python program to determine if an undirected graph is bipartite using BFS.

Python Program to Check if Undirected Graph is Bipartite using BFS

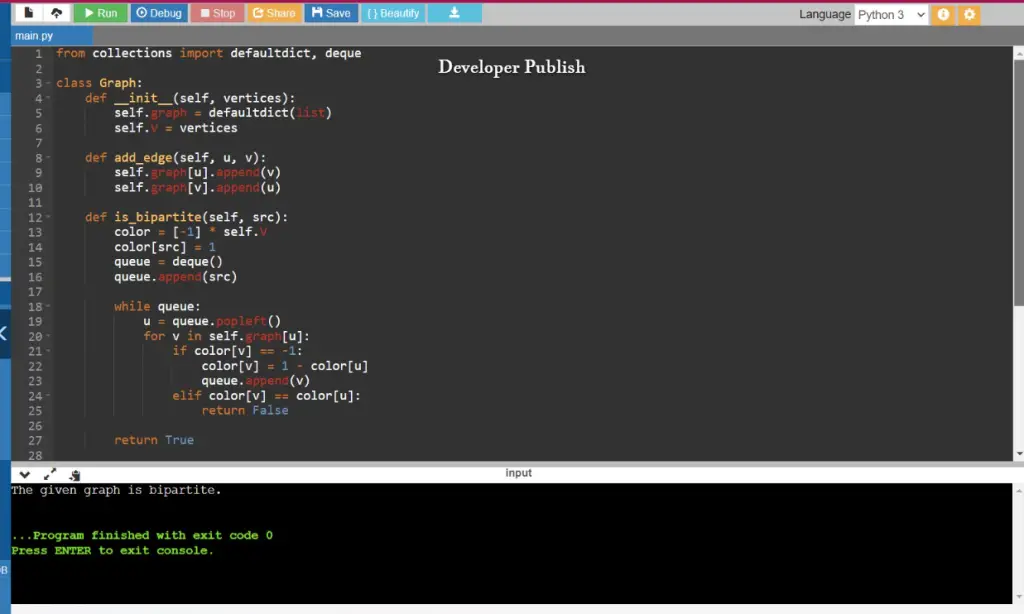
from collections import defaultdict, deque

class Graph:
    def __init__(self, vertices):
        self.graph = defaultdict(list)
        self.V = vertices

    def add_edge(self, u, v):
        self.graph[u].append(v)
        self.graph[v].append(u)

    def is_bipartite(self, src):
        color = [-1] * self.V
        color[src] = 1
        queue = deque()
        queue.append(src)

        while queue:
            u = queue.popleft()
            for v in self.graph[u]:
                if color[v] == -1:
                    color[v] = 1 - color[u]
                    queue.append(v)
                elif color[v] == color[u]:
                    return False

        return True

def is_bipartite_graph(graph):
    g = Graph(len(graph))
    for u, neighbors in enumerate(graph):
        for v in neighbors:
            g.add_edge(u, v)

    return g.is_bipartite(0)  # Start BFS from the first vertex

# Example usage:
if __name__ == "__main__":
    graph = [[1, 3], [0, 2], [1, 3], [0, 2]]
    if is_bipartite_graph(graph):
        print("The given graph is bipartite.")
    else:
        print("The given graph is not bipartite.")

How It Works

1. We represent the graph as an adjacency list using defaultdict.
2. We create a function is_bipartite that takes the source vertex as an argument and performs a BFS traversal of the graph while assigning colors (0 or 1) to vertices.
3. If at any point during BFS, we encounter an adjacent vertex with the same color as the current vertex, the graph is not bipartite, and we return False.
4. If the BFS traversal completes without any conflicts in vertex coloring, we return True.
5. The is_bipartite_graph function converts the given graph into the Graph class and starts BFS from the first vertex.

Input/Output