C Program to Check whether a Number is Prime or Not using Recursion

This C program checks whether a given number is prime or not using a recursive approach. A prime number is a positive integer greater than 1 that has no positive integer divisors other than 1 and itself.

Prime numbers are positive integers greater than 1 that have no positive divisors other than 1 and themselves. In other words, a prime number is a number that cannot be evenly divided by any other number except 1 and itself.

Problem Statement

Write a program in C to check if the given number is a prime number or not using Recurssion.

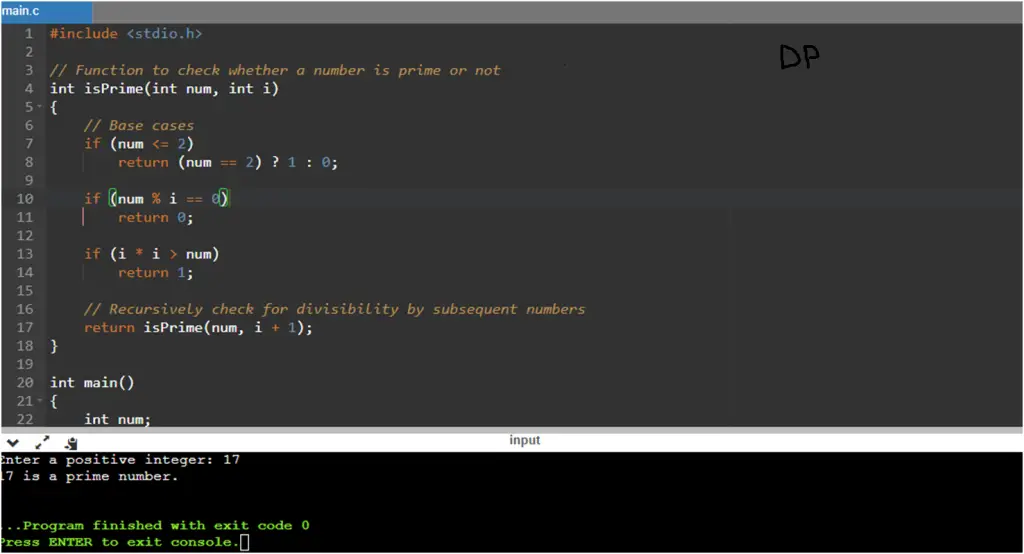
C Program to Check whether a Number is Prime or Not using Recursion

#include <stdio.h>

// Function to check whether a number is prime or not
int isPrime(int num, int i)
{
    // Base cases
    if (num <= 2)
        return (num == 2) ? 1 : 0;
    
    if (num % i == 0)
        return 0;
    
    if (i * i > num)
        return 1;
    
    // Recursively check for divisibility by subsequent numbers
    return isPrime(num, i + 1);
}

int main()
{
    int num;

    printf("Enter a positive integer: ");
    scanf("%d", &num);

    // Call the isPrime function
    if (isPrime(num, 2))
        printf("%d is a prime number.\n", num);
    else
        printf("%d is not a prime number.\n", num);

    return 0;
}

How it works

1. The program prompts the user to enter a positive integer.
2. The user enters a positive integer num.
3. The main function calls the isPrime function with the arguments num and 2.
4. The isPrime function is a recursive function that checks whether num is prime or not.
5. Inside the isPrime function, there are several base cases and conditions:
   • If num is less than or equal to 2, the function returns 1 if num is equal to 2 (since 2 is a prime number) or 0 otherwise.
   • If num is divisible by the current divisor i (where i starts from 2 and increments in subsequent recursive calls), the function returns 0 (indicating that num is not prime).
   • If i * i is greater than num, it means that we have checked divisibility by all possible divisors up to the square root of num, and the function returns 1 (indicating that num is prime).
   • If none of the above conditions are met, the function calls itself recursively with an incremented i.
6. The recursion continues until one of the base cases is reached or the conditions for prime checking are met.
7. Once the recursion ends, the main function checks the return value of the isPrime function.
   • If the return value is 1, the program outputs that num is a prime number.
   • If the return value is 0, the program outputs that num is not a prime number.
8. The program terminates.

By using recursion, the program divides the problem of prime number checking into smaller subproblems, recursively checking for divisibility by subsequent numbers. This approach simplifies the logic and avoids the need for a loop.

Input/Output