Python Program to Find the Fibonacci Series Without using Recursion

This Python program generates the Fibonacci series without using recursion. It calculates and displays the first n Fibonacci numbers using iteration.

The Fibonacci series is a sequence of numbers in which each number is the sum of the two preceding ones. It starts with 0 and 1, and the subsequent numbers are obtained by adding the last two numbers in the sequence. The Fibonacci series typically begins as follows: 0, 1, 1, 2, 3, 5, 8, 13, 21, and so on.

Program Statement

Given an integer n, we need to generate the first n Fibonacci numbers without using recursion and display them as a list.

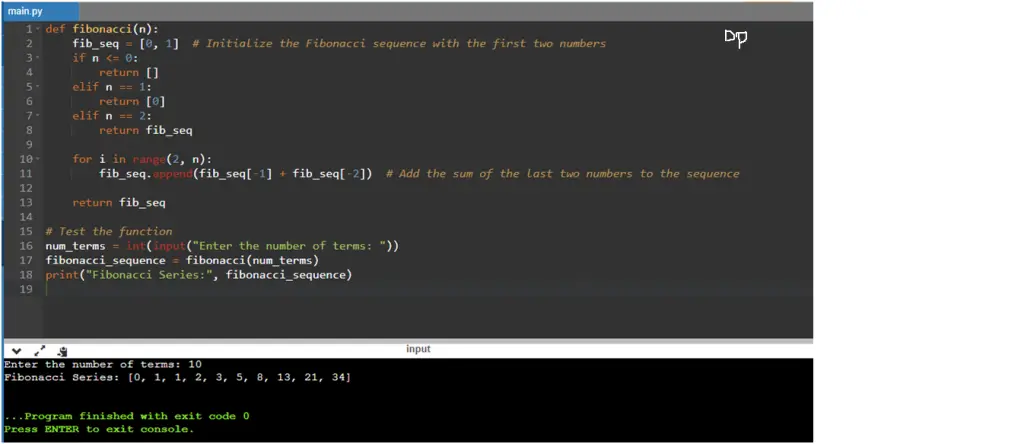
Python Program to Find the Fibonacci Series Without using Recursion

def fibonacci(n):
    fib_seq = [0, 1]  # Initialize the Fibonacci sequence with the first two numbers
    if n <= 0:
        return []
    elif n == 1:
        return [0]
    elif n == 2:
        return fib_seq
    
    for i in range(2, n):
        fib_seq.append(fib_seq[-1] + fib_seq[-2])  # Add the sum of the last two numbers to the sequence

    return fib_seq

# Test the function
num_terms = int(input("Enter the number of terms: "))
fibonacci_sequence = fibonacci(num_terms)
print("Fibonacci Series:", fibonacci_sequence)

This program asks the user to input the number of terms they want in the Fibonacci series. It then uses the fibonacci() function to generate the series without recursion. The function initializes the Fibonacci sequence with the first two numbers, [0, 1], and then iteratively calculates the next number by adding the last two numbers in the sequence. Finally, it returns the generated Fibonacci series.

The program prints the Fibonacci series for the specified number of terms. You can run the program, provide the number of terms you want, and it will output the Fibonacci series without using recursion.

How it works

1. The program defines a function called fibonacci() that takes an input n representing the number of terms in the Fibonacci series to be generated.
2. Inside the fibonacci() function, we initialize a list called fib_seq with the first two numbers of the Fibonacci series, [0, 1].
3. The function checks for special cases. If n is less than or equal to 0, it returns an empty list. If n is 1, it returns [0], and if n is 2, it returns the initial Fibonacci sequence [0, 1].
4. If n is greater than 2, the function enters a loop that iterates n-2 times (since we already have the first two numbers in the sequence).
5. Inside the loop, the function calculates the next Fibonacci number by adding the last two numbers in the fib_seq list (fib_seq[-1] and fib_seq[-2]). It appends this sum to the fib_seq list.
6. After the loop completes, the function returns the generated Fibonacci sequence stored in the fib_seq list.
7. The program prompts the user to enter the number of terms they want in the Fibonacci series using the input() function, and the input is stored in the variable num_terms.
8. The program calls the fibonacci() function with num_terms as the argument, and the result is stored in the variable fibonacci_sequence.
9. Finally, the program prints the generated Fibonacci series by displaying the contents of the fibonacci_sequence list using the print() function.

By following these steps, the program generates the Fibonacci series without using recursion. It uses an iterative approach to efficiently calculate and store the Fibonacci numbers based on the number of terms specified by the user.

Input/Output