Python Program to Find Fibonacci Numbers using Recursion

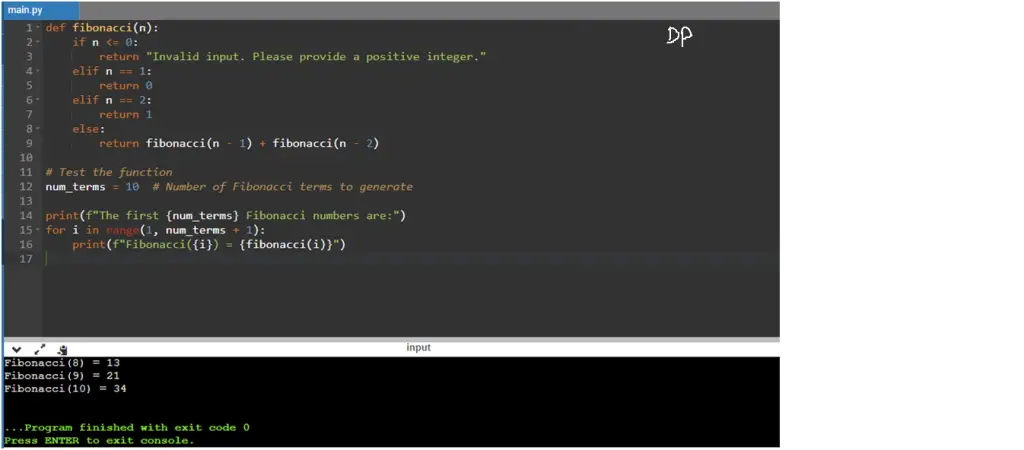
This Python program uses recursion to generate the first n Fibonacci numbers and displays them in a list.

Program Statement

Given an integer n, we need to find the first n Fibonacci numbers using recursion and display them in a list.

Python Program to Find Fibonacci Numbers using Recursion

def fibonacci(n):
    if n <= 0:
        return "Invalid input. Please provide a positive integer."
    elif n == 1:
        return 0
    elif n == 2:
        return 1
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

# Test the function
num_terms = 10  # Number of Fibonacci terms to generate

print(f"The first {num_terms} Fibonacci numbers are:")
for i in range(1, num_terms + 1):
    print(f"Fibonacci({i}) = {fibonacci(i)}")

How it works

1. The fibonacci function is defined, which takes an integer n as input and returns the Fibonacci number at position n.
2. The function checks for the base cases:
   • If n is less than or equal to 0, it returns an error message stating that the input is invalid.
   • If n is 1, it returns 0 since the first Fibonacci number is 0.
   • If n is 2, it returns 1 since the second Fibonacci number is 1.
3. If n is greater than 2, the function recursively calls itself with n-1 and n-2 as arguments and returns the sum of the two resulting function calls: fibonacci(n-1) + fibonacci(n-2). This step repeats until the base cases are reached.
4. In the main part of the program, a variable num_terms is set to the number of Fibonacci terms to generate.
5. A loop is used to iterate from 1 to num_terms. In each iteration, the loop prints the Fibonacci number at the current position by calling the fibonacci function with the current iteration value.
6. The program executes and prints the first num_terms Fibonacci numbers.

By using recursion, the fibonacci function repeatedly breaks down the problem of finding the nth Fibonacci number into simpler subproblems until it reaches the base cases. The function then combines the results of the subproblems to calculate the Fibonacci number at position n.

Input/Output