Python Program to Find All Perfect Squares in the Given Range

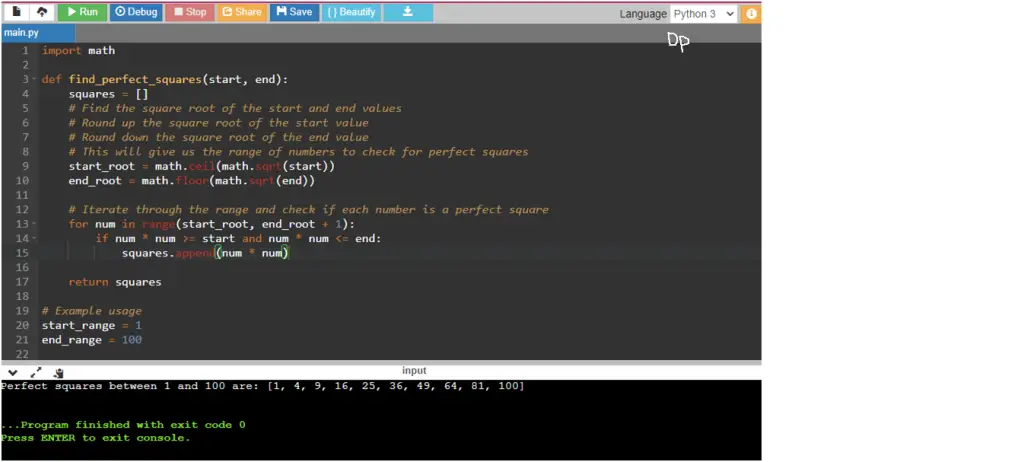
This Python program finds all perfect squares within a given range (inclusive) and displays them as a list. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. For example, 4, 9, 16, and 25 are perfect squares because they can be expressed as 2×2, 3×3, 4×4, and 5×5, respectively.

Program Statement

Given a range specified by the start and end values, we need to find all perfect squares within that range (including both the start and end values) and display them as a list.

Python Program to Find All Perfect Squares in the Given Range

import math

def find_perfect_squares(start, end):
    squares = []
    # Find the square root of the start and end values
    # Round up the square root of the start value
    # Round down the square root of the end value
    # This will give us the range of numbers to check for perfect squares
    start_root = math.ceil(math.sqrt(start))
    end_root = math.floor(math.sqrt(end))

    # Iterate through the range and check if each number is a perfect square
    for num in range(start_root, end_root + 1):
        if num * num >= start and num * num <= end:
            squares.append(num * num)

    return squares

# Example usage
start_range = 1
end_range = 100

result = find_perfect_squares(start_range, end_range)
print("Perfect squares between", start_range, "and", end_range, "are:", result)

How it works

1. Import the math module, which provides mathematical functions including square root calculation.
2. Define a function called find_perfect_squares that takes two parameters: start and end.
3. Inside the function, initialize an empty list called squares to store the perfect squares.
4. Calculate the square root of the start value using math.sqrt() and round it up using math.ceil(). Assign the result to start_root.
5. Calculate the square root of the end value using math.sqrt() and round it down using math.floor(). Assign the result to end_root.
6. Iterate through the range from start_root to end_root + 1.
7. For each number in the range, check if its square falls within the given range (start and end).
8. If the square of the number falls within the range, append it to the squares list.
9. After iterating through all the numbers, return the squares list.
10. Outside the function, prompt the user to enter the start_range and end_range values.
11. Call the find_perfect_squares function with the entered start_range and end_range values, and assign the result to a variable result.
12. Print the start and end range values.
13. Print the list of perfect squares found within the range.

The program calculates the square root of the start and end values to determine the range of numbers to check for perfect squares. It then iterates through this range, checks if each number squared falls within the given range, and appends the perfect squares to a list. Finally, it displays the list of perfect squares found within the given range.

Input/Output