Python Program to Check Whether a Given Number is Perfect Number

A perfect number is a positive integer that is equal to the sum of its proper divisors, excluding itself. For example, the number 28 is a perfect number because its divisors (excluding itself) are 1, 2, 4, 7, and 14, and their sum is 28.

Here’s a Python program to check whether a given number is a perfect number:

Problem Statement

Write a Python program that checks whether a given number is a perfect number or not. A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding itself).

Your program should include the following:

1. A function named is_perfect_number that takes an integer number as input.
2. The function should return True if the number is a perfect number, and False otherwise.
3. Proper divisors are the positive divisors of a number excluding the number itself.
4. The program should prompt the user to enter a number.
5. After receiving the input, the program should call the is_perfect_number function to check if the number is perfect.
6. Finally, the program should display an appropriate message indicating whether the number is perfect or not.

Python Program to Check Whether a Given Number is Perfect Number

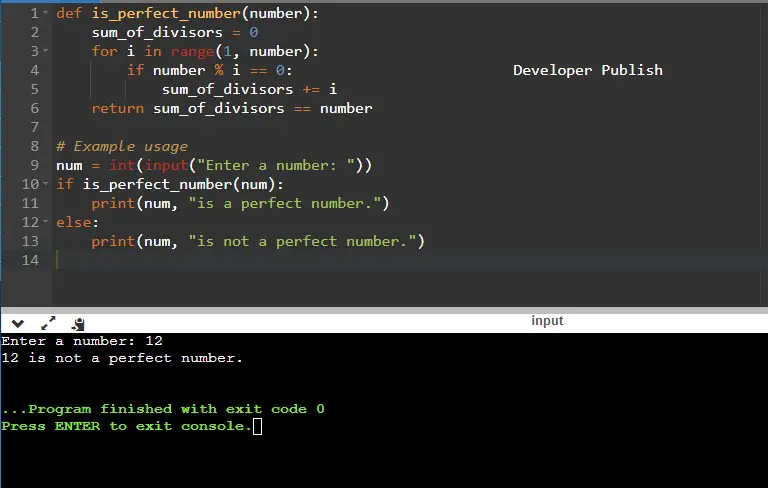
def is_perfect_number(number):
    sum_of_divisors = 0
    for i in range(1, number):
        if number % i == 0:
            sum_of_divisors += i
    return sum_of_divisors == number

# Example usage
num = int(input("Enter a number: "))
if is_perfect_number(num):
    print(num, "is a perfect number.")
else:
    print(num, "is not a perfect number.")

How it Works

1. The program starts by defining a function called is_perfect_number that takes an integer number as input. This function will determine whether the given number is a perfect number or not.
2. Within the is_perfect_number function, a variable called sum_of_divisors is initialized to 0. This variable will store the sum of the proper divisors of the number.
3. A for loop is used to iterate over the range from 1 to number - 1. This loop will check each number as a potential divisor of the given number.
4. Inside the loop, an if statement checks if the current number is a divisor of number. This is done by checking if number modulo i equals 0. If it does, then i is a divisor.
5. If i is a divisor, it is added to the sum_of_divisors using the += operator.
6. After the loop completes, the sum_of_divisors is compared with the original number. If they are equal, it means the number is a perfect number, and the function returns True.
7. If the sum_of_divisors is not equal to the number, the function returns False, indicating that the number is not perfect.
8. In the main part of the program, the user is prompted to enter a number using the input() function.
9. The input is then converted to an integer using the int() function and stored in the num variable.
10. The is_perfect_number function is called with the num variable as an argument to check whether it is a perfect number or not.
11. Depending on the returned value from the is_perfect_number function, an appropriate message is displayed using the print() function to indicate whether the number is perfect or not.
12. The program terminates after displaying the result for one number.

That’s how the program works! It calculates the sum of proper divisors and compares it with the original number to determine if it is a perfect number.

Input/ Output