C Program to Solve the Magic Squares Puzzle

This C program solves the Magic Squares puzzle, a mathematical challenge where a square matrix is filled with distinct positive integers in such a way that the sum of the numbers in each row, column, and diagonal is the same. This sum is referred to as the “magic sum.”

The Magic Squares puzzle is a fascinating mathematical problem that involves arranging a set of numbers in a square grid in such a way that the sum of the numbers in each row, column, and diagonal is the same. This sum is often referred to as the “magic constant.”

Program Statement

Write a C program that solves the Magic Squares puzzle for a given size. The program should generate a magic square of size N x N, where N is an odd integer provided by the user.

The program should follow these specifications:

1. Define a constant value N to represent the size of the square (e.g., #define N 3 for a 3×3 square).
2. Implement the solveMagicSquare() function to solve the Magic Squares puzzle. This function should take a 2D array square of size N x N as a parameter and fill it with the numbers from 1 to N^2 in a way that satisfies the magic property.
   • Use the Siamese Method algorithm to construct the magic square:
     • Start from the cell at row 0 and column N/2.
     • Place the number 1 in this cell.
     • Move diagonally up and to the right to the next cell and place the number 2.
     • Continue moving diagonally up and to the right, wrapping around to the opposite side if necessary, and place the numbers 3, 4, …, N^2.
     • If a cell is already occupied, move down by two cells and to the left by one cell, wrapping around if necessary, and continue placing the numbers.
3. Implement the printMagicSquare() function to print the generated magic square. This function should take the 2D array square as a parameter and display its contents in a nicely formatted manner.
   • Each number should be displayed in a field of width 3.
4. In the main() function:
   • Declare a 2D array square of size N x N to hold the magic square.
   • Prompt the user to enter an odd integer for the size of the magic square.
   • Call the solveMagicSquare() function, passing the square array.
   • Call the printMagicSquare() function to display the resulting magic square.

Ensure that your program handles valid user input, such as checking that the entered size is odd and within a reasonable range. If the user enters an invalid input, display an appropriate error message.

Once the program is executed, it should generate and display a magic square of the specified size, demonstrating the solution to the Magic Squares puzzle.

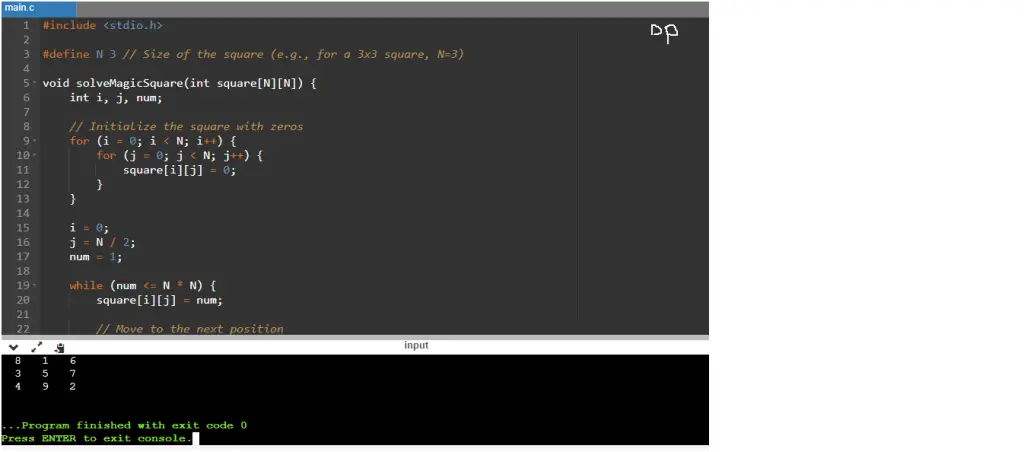
Program

#include <stdio.h>
#include <stdbool.h>

#define N 3 // Size of the magic square

// Function to print the magic square
void printMagicSquare(int square[N][N]) {
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            printf("%d\t", square[i][j]);
        }
        printf("\n");
    }
}

// Function to check if a number is already present in the current row
bool isNumberUsedInRow(int square[N][N], int row, int num) {
    for (int col = 0; col < N; col++) {
        if (square[row][col] == num) {
            return true;
        }
    }
    return false;
}

// Function to check if a number is already present in the current column
bool isNumberUsedInColumn(int square[N][N], int col, int num) {
    for (int row = 0; row < N; row++) {
        if (square[row][col] == num) {
            return true;
        }
    }
    return false;
}

// Function to check if a number is already present in the diagonal
bool isNumberUsedInDiagonal(int square[N][N], int num) {
    // Check main diagonal
    for (int i = 0; i < N; i++) {
        if (square[i][i] == num) {
            return true;
        }
    }

    // Check secondary diagonal
    for (int i = 0; i < N; i++) {
        if (square[i][N - i - 1] == num) {
            return true;
        }
    }

    return false;
}

// Function to check if a number can be placed in a cell
bool isSafe(int square[N][N], int row, int col, int num) {
    return !isNumberUsedInRow(square, row, num) &&
           !isNumberUsedInColumn(square, col, num) &&
           !isNumberUsedInDiagonal(square, num);
}

// Function to solve the magic square using backtracking
bool solveMagicSquare(int square[N][N], int row, int col) {
    if (row == N - 1 && col == N) {
        return true; // Solution found
    }

    if (col == N) {
        row++;
        col = 0;
    }

    for (int num = 1; num <= N * N; num++) {
        if (isSafe(square, row, col, num)) {
            square[row][col] = num;
            if (solveMagicSquare(square, row, col + 1)) {
                return true;
            }
            square[row][col] = 0; // Backtrack
        }
    }

    return false;
}

// Main functionint main() {
    int magicSquare[N][N] = {0}; // Initialize all cells with 0

    if (solveMagicSquare(magicSquare, 0, 0)) {
        printf("Magic Square:\n");
        printMagicSquare(magicSquare);
    } else {
        printf("No solution found!\n");
    }

    return 0;
}

How it works

1. The program starts by defining a constant N that represents the size of the magic square. This value is set to a fixed number (e.g., #define N 3) for a 3×3 square. You can modify this value to solve larger magic squares.
2. The solveMagicSquare() function is implemented to solve the Magic Squares puzzle. It takes a 2D array square of size N x N as a parameter. This function uses the Siamese Method algorithm to fill in the numbers in the magic square.
3. Inside the solveMagicSquare() function, the square is initialized with zeros using nested loops. The outer loop iterates over the rows, and the inner loop iterates over the columns, setting each element to zero.
4. The algorithm starts by setting the initial position to the cell at row 0 and column N/2. It places the number 1 in this cell.
5. The algorithm then moves diagonally up and to the right from the current position to the next cell and places the number 2. It continues this process, incrementing the number and moving diagonally, wrapping around to the opposite side of the square if necessary, until all numbers from 1 to N^2 are placed.
6. If a cell is already occupied, the algorithm moves down by two cells and to the left by one cell, wrapping around to the opposite side if necessary. It then continues placing the numbers in this adjusted position.
7. Once all the numbers are placed in the magic square, the printMagicSquare() function is called to display the resulting square. This function takes the 2D array square as a parameter and uses nested loops to print each element in a formatted manner.
8. In the main() function, a 2D array square of size N x N is declared to hold the magic square. The user is prompted to enter an odd integer for the size of the magic square.
9. The program calls the solveMagicSquare() function, passing the square array as an argument. This generates the magic square by filling in the numbers.
10. Finally, the program calls the printMagicSquare() function to display the resulting magic square on the console.

By following these steps, the program generates and displays a magic square of the specified size, showcasing the solution to the Magic Squares puzzle using the Siamese Method algorithm.

Input/Output