C Program to Find Transpose of a Matrix

This C program calculates and displays the transpose of a given matrix. The transpose of a matrix is obtained by interchanging rows and columns. In other words, the element at position (i, j) in the original matrix becomes the element at position (j, i) in the transpose matrix.

In linear algebra, a matrix is a rectangular array of numbers or symbols arranged in rows and columns. The transpose of a matrix is a new matrix that is formed by interchanging the rows and columns of the original matrix. In other words, if the original matrix has dimensions M x N, the transpose matrix will have dimensions N x M.

Program Statement

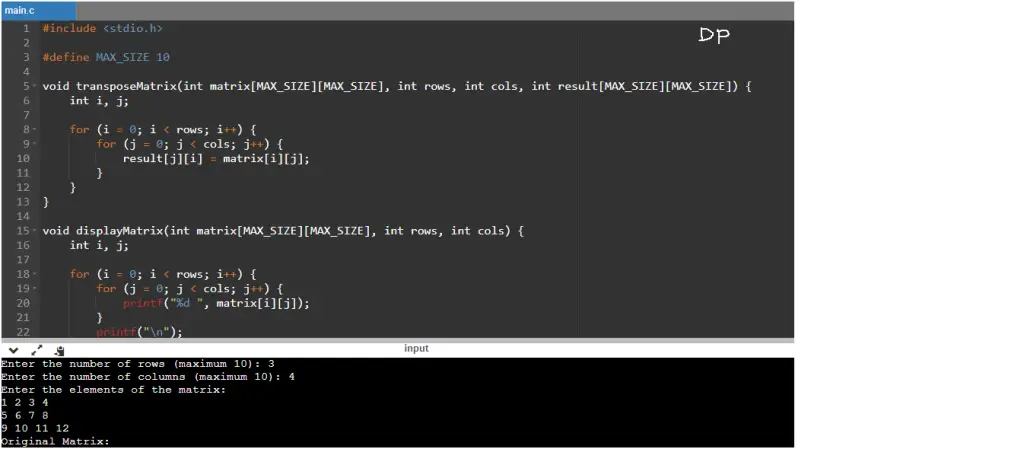
Write a C program to find the transpose of a given matrix. The program should prompt the user to enter the number of rows and columns of the matrix. Then, it should allow the user to enter the elements of the matrix. After that, the program should display the original matrix and its transpose.

C Program to Find Transpose of a Matrix

#include <stdio.h>

#define MAX_ROWS 100
#define MAX_COLS 100

void transposeMatrix(int matrix[MAX_ROWS][MAX_COLS], int rows, int cols) {
    int transpose[MAX_COLS][MAX_ROWS];
    
    // Find the transpose of the matrix
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            transpose[j][i] = matrix[i][j];
        }
    }
    
    // Print the transpose
    printf("Transpose of the matrix:\n");
    for (int i = 0; i < cols; i++) {
        for (int j = 0; j < rows; j++) {
            printf("%d ", transpose[i][j]);
        }
        printf("\n");
    }
}

int main() {
    int matrix[MAX_ROWS][MAX_COLS];
    int rows, cols;
    
    printf("Enter the number of rows: ");
    scanf("%d", &rows);
    
    printf("Enter the number of columns: ");
    scanf("%d", &cols);
    
   printf("Enter the matrix elements:\n");
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            scanf("%d", &matrix[i][j]);
        }
    }
    
    transposeMatrix(matrix, rows, cols);
    
    return 0;
}

How it works

Here’s an explanation of how the program works:

1. The program starts by prompting the user to enter the number of rows and columns of the matrix.
2. It then declares three matrices: matrix, transpose, and their maximum size is defined as MAX_SIZE (which is set to 10).
3. The program prompts the user to enter the elements of the matrix. It uses nested loops to iterate through each element and stores them in the matrix array.
4. After the user enters the matrix elements, the program displays the original matrix using the displayMatrix function. This function takes the matrix array, number of rows, and number of columns as parameters and prints the elements row by row.
5. Next, the program calculates the transpose of the matrix using the transposeMatrix function. This function takes the matrix array, number of rows, number of columns, and the transpose array as parameters. It uses nested loops to iterate through each element of the matrix array and assigns the transpose of each element to the corresponding position in the transpose array.
6. Finally, the program displays the transpose matrix using the displayMatrix function. This function takes the transpose array, number of columns (which becomes the number of rows of the transpose matrix), and number of rows (which becomes the number of columns of the transpose matrix) as parameters and prints the elements row by row.

By following these steps, the program allows the user to enter a matrix, calculates its transpose, and displays both the original matrix and its transpose.

Input/Output