C Program to Find the Roots of a Quadratic Equation

This C program calculates the roots of a quadratic equation of the form ax^2 + bx + c = 0.

Quadratic equations play a vital role in mathematics and physics, and finding their roots is a fundamental operation. A quadratic equation is an equation of the form ax² + bx + c = 0, where a, b, and c are constants. In this program, we will write a C program to calculate the roots of a quadratic equation using the quadratic formula.

Problem statement

We need to develop a C program that takes input values for the coefficients a, b, and c of a quadratic equation and calculates its roots. The program should handle different scenarios, such as real and distinct roots, real and equal roots, and imaginary roots.

C Program to Find the Roots of a Quadratic Equation

#include <stdio.h>
#include <math.h>

int main()
{
    double a, b, c, discriminant, root1, root2, realPart, imaginaryPart;

    printf("Enter coefficients a, b, and c: ");
    scanf("%lf %lf %lf", &a, &b, &c);

    discriminant = b * b - 4 * a * c;

    if (discriminant > 0)
    {
        root1 = (-b + sqrt(discriminant)) / (2 * a);
        root2 = (-b - sqrt(discriminant)) / (2 * a);
        printf("Roots are real and different.\n");
        printf("Root 1 = %.2lf\n", root1);
        printf("Root 2 = %.2lf\n", root2);
    }
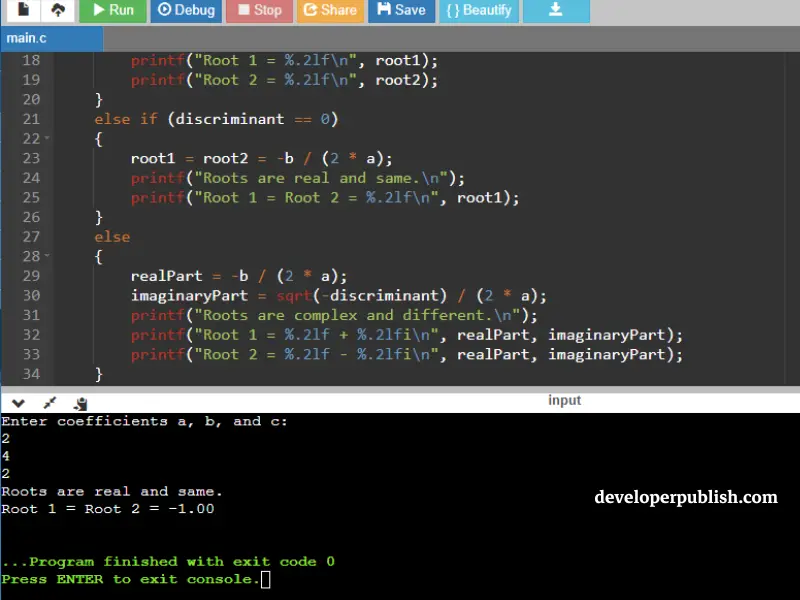
    else if (discriminant == 0)
    {
        root1 = root2 = -b / (2 * a);
        printf("Roots are real and same.\n");
        printf("Root 1 = Root 2 = %.2lf\n", root1);
    }
    else
    {
        realPart = -b / (2 * a);
        imaginaryPart = sqrt(-discriminant) / (2 * a);
        printf("Roots are complex and different.\n");
        printf("Root 1 = %.2lf + %.2lfi\n", realPart, imaginaryPart);
        printf("Root 2 = %.2lf - %.2lfi\n", realPart, imaginaryPart);
    }

    return 0;
}

How It Works

1. The program begins by including the necessary header files: <stdio.h> for input/output operations and <math.h> for mathematical functions like sqrt().
2. Inside the main() function, variables are declared to store the coefficients (a, b, c), the discriminant (discriminant), and the roots (root1, root2) of the quadratic equation. There are also variables to store the real and imaginary parts of the roots in case they are complex (realPart, imaginaryPart).
3. The user is prompted to enter the values of coefficients a, b, and c using printf() and scanf() functions.
4. The discriminant of the quadratic equation is calculated using the formula b * b - 4 * a * c. The value of the discriminant determines the nature of the roots.
5. Using conditional statements (if, else if, else), the program checks the value of the discriminant to determine the type of roots.
6. If the discriminant is greater than 0, it means the roots are real and different. The program calculates the roots using the quadratic formula ((-b + sqrt(discriminant)) / (2 * a) and (-b - sqrt(discriminant)) / (2 * a)) and displays them using printf().
7. If the discriminant is equal to 0, it means the roots are real and equal. The program calculates the root using the formula root1 = root2 = -b / (2 * a) and displays it.
8. If the discriminant is less than 0, it means the roots are complex. The program calculates the real and imaginary parts of the roots using the formulas realPart = -b / (2 * a) and imaginaryPart = sqrt(-discriminant) / (2 * a). It then displays the roots in the form realPart + imaginaryPart i and realPart - imaginaryPart i using printf().
9. Finally, the program ends by returning 0 from the main() function.

Input\Output