C Program to Reverse a Stack using Recursion

This C program demonstrates how to reverse a stack using recursion. A stack is a linear data structure that follows the Last-In-First-Out (LIFO) principle. Reversing a stack involves changing the order of its elements such that the top element becomes the bottom element, and so on.

Reversing a stack means changing the order of its elements so that the topmost element becomes the bottom-most and vice versa. One way to reverse a stack is by using recursion. Recursion is a programming technique where a function calls itself to solve a smaller subproblem. In the case of reversing a stack, the idea is to recursively pop all the elements from the stack, reverse the remaining stack, and then insert the popped element at the bottom of the reversed stack.

Problem Statement

Write a C program to reverse a stack using recursion. Given a stack of integers, the program should reverse the order of its elements using recursion and display the reversed stack.

Input:

• The input is a stack of integers.

Output:

• The program should display the original stack and the reversed stack.

Constraints:

• The maximum number of elements in the stack is fixed at 100.
• The input stack may contain duplicates and can be empty.

C Program to Reverse a Stack using Recursion

#include <stdio.h>
#include <stdlib.h>

#define MAX_SIZE 100

// Structure to represent a stack
struct Stack {
    int arr[MAX_SIZE];
    int top;
};

// Function to initialize a stack
void initialize(struct Stack *s) {
    s->top = -1;
}

// Function to check if the stack is empty
int isEmpty(struct Stack *s) {
    return s->top == -1;
}

// Function to check if the stack is full
int isFull(struct Stack *s) {
    return s->top == MAX_SIZE - 1;
}

// Function to push an element onto the stack
void push(struct Stack *s, int data) {
    if (isFull(s)) {
        printf("Stack overflow!\n");
        return;
    }
    s->arr[++(s->top)] = data;
}

// Function to pop an element from the stack
int pop(struct Stack *s) {
    if (isEmpty(s)) {
        printf("Stack underflow!\n");
        return -1;
    }
    return s->arr[(s->top)--];
}

// Function to insert an element at the bottom of the stack
void insertAtBottom(struct Stack *s, int data) {
    if (isEmpty(s)) {
        push(s, data);
        return;
    }

    int temp = pop(s);
    insertAtBottom(s, data);
    push(s, temp);
}

// Function to reverse a stack using recursion
void reverseStack(struct Stack *s) {
    if (isEmpty(s))
        return;

    int temp = pop(s);
    reverseStack(s);
    insertAtBottom(s, temp);
}

// Function to display the elements of the stack
void display(struct Stack *s) {
    if (isEmpty(s)) {
        printf("Stack is empty!\n");
        return;
    }

    printf("Stack elements: ");
    for (int i = 0; i <= s->top; i++) {
        printf("%d ", s->arr[i]);
    }
    printf("\n");
}

// Main function
int main() {
    struct Stack s;
    initialize(&s);

    push(&s, 1);
    push(&s, 2);
    push(&s, 3);
    push(&s, 4);
    push(&s, 5);

    printf("Original ");
    display(&s);

    reverseStack(&s);

    printf("Reversed ");
    display(&s);

    return 0;
}

How it Works

The program works by using recursion to reverse a stack. Here’s a step-by-step explanation of how it works:

1. The program defines a structure called Stack, which represents the stack data structure. It has an array arr to store the elements and a variable top to keep track of the topmost element.
2. The program provides various functions to work with the stack:
   • initialize: Initializes the stack by setting the top index to -1.
   • isEmpty: Checks if the stack is empty by comparing the top index with -1.
   • isFull: Checks if the stack is full by comparing the top index with the maximum size of the stack.
   • push: Pushes an element onto the stack. It first checks if the stack is full to avoid overflow.
   • pop: Pops and returns the top element from the stack. It first checks if the stack is empty to avoid underflow.
   • insertAtBottom: Inserts an element at the bottom of the stack using recursion. If the stack is empty, it directly pushes the element onto the stack. Otherwise, it recursively pops an element, calls itself to insert the element at the bottom of the remaining stack, and then pushes the popped element back onto the stack.
   • reverseStack: Reverses the stack using recursion. If the stack is empty, it returns. Otherwise, it pops the top element, recursively calls itself to reverse the remaining stack, and then inserts the popped element at the bottom of the reversed stack using the insertAtBottom function.
   • display: Displays the elements of the stack.
3. In the main function, the program creates a stack using the initialize function.
4. It pushes some elements onto the stack using the push function.
5. The original stack is displayed using the display function.
6. The reverseStack function is called to reverse the stack using recursion.
7. The reversed stack is displayed using the display function.

By recursively popping elements from the original stack, reversing the remaining stack, and inserting the popped elements at the bottom of the reversed stack, the program effectively reverses the order of the elements in the stack.

The recursion continues until the stack is empty, and then the reversed stack is displayed.

Input /Output

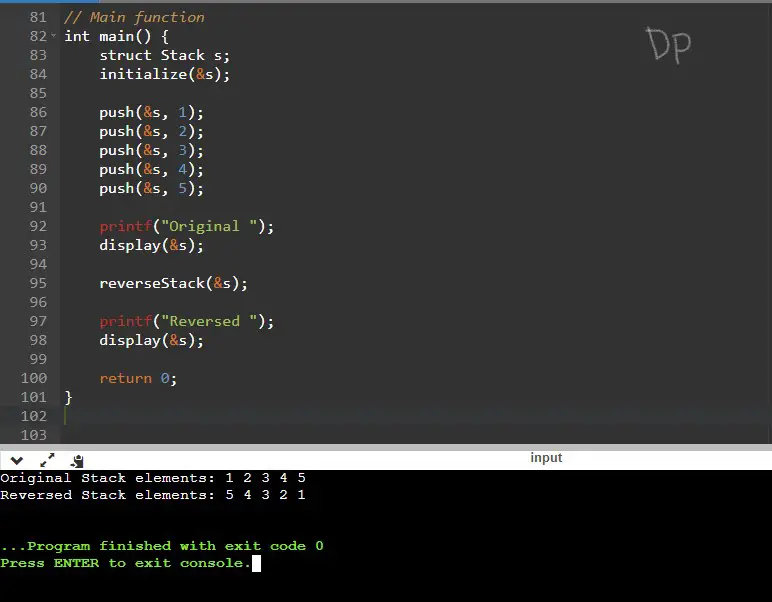
Explanation:

• The input stack contains the elements 5, 4, 3, 2, and 1 in the order they were inserted.
• The program displays the original stack as “5 4 3 2 1” using the display function.
• Then, the program calls the reverseStack function to reverse the stack.
• Inside the reverseStack function, the top element (5) is popped from the stack.
• The function recursively calls itself with the remaining stack elements (4, 3, 2, and 1).
• The recursive call further pops the top element (4) and calls itself again with the remaining elements (3, 2, and 1).
• This process continues until the stack is empty.
• Now, the function starts inserting the popped elements at the bottom of the reversed stack using the insertAtBottom function.
• The insertAtBottom function inserts the element 1 at the bottom of the empty stack.
• The reverseStack function continues inserting the remaining elements (2, 3, 4, and 5) in reverse order.
• Finally, the program displays the reversed stack as “1 2 3 4 5” using the display function.