C Program to Find Sum of N Numbers using Recursion

This C program calculates the sum of the first N natural numbers using recursion.

Problem Statement

The program should perform the following steps:

1. Prompt the user to enter the value of N.
2. Read the input value of N from the user.
3. Define a recursive function called findSum that takes an integer n as an argument and returns the sum of the first n numbers.
4. Inside the findSum function, implement two cases:
   • Base case: If n is equal to 0, return 0.
   • Recursive case: If n is not 0, recursively call findSum with the argument n - 1, and add n to the result of the recursive call.
5. In the main function, call the findSum function with N as the argument and store the returned sum.
6. Display the sum of the first N numbers to the user.

Ensure that your program handles valid inputs and produces the correct sum of the numbers.

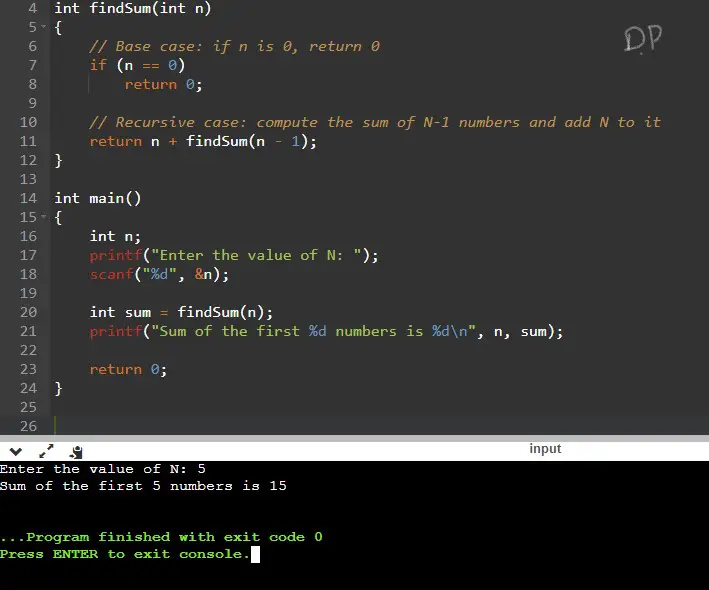
C Program to Find Sum of N Numbers using Recursion

#include <stdio.h>

// Function to find the sum of N numbers using recursion
int findSum(int n)
{
    // Base case: if n is 0, return 0
    if (n == 0)
        return 0;
    
    // Recursive case: compute the sum of N-1 numbers and add N to it
    return n + findSum(n - 1);
}

int main()
{
    int n;
    printf("Enter the value of N: ");
    scanf("%d", &n);
    
    int sum = findSum(n);
    printf("Sum of the first %d numbers is %d\n", n, sum);
    
    return 0;
}

How it Works

1. The program starts by prompting the user to enter the value of N.
2. The user enters a positive integer N, indicating the number of elements to sum.
3. The program reads the input value of N from the user.
4. The program then calls the findSum function, passing the value of N as an argument.
5. Inside the findSum function, two cases are implemented:
   • Base case: If the value of n is equal to 0, the function returns 0. This serves as the termination condition for the recursion, as the sum of 0 numbers is 0.
   • Recursive case: If n is not 0, the function recursively calls itself with the argument n - 1. This means that the function will compute the sum of the first n-1 numbers.
     • In this recursive call, the function eventually reaches the base case when n becomes 0, and the recursion ends.
     • The function then adds n to the result of the recursive call, effectively summing the first n numbers.
6. The findSum function returns the sum to the main function.
7. The sum is stored in a variable called sum.
8. Finally, the program displays the sum of the first N numbers to the user.

By using recursion, the program repeatedly breaks down the problem of finding the sum of N numbers into smaller subproblems until it reaches a base case. Then, it combines the results of the subproblems to obtain the final sum

Input /Output