C Program to Convert Binary to Gray Code using Recursion

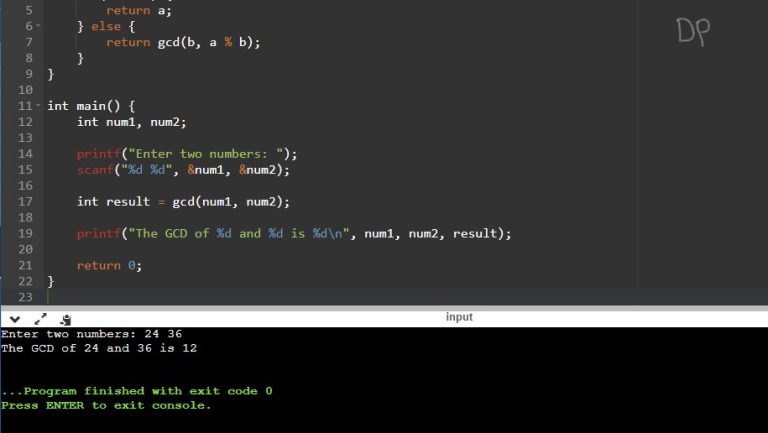
This C program converts a binary number to its corresponding Gray code using recursion.

Binary Code: Binary code is a number system that uses only two digits, 0 and 1. It is the basis of all digital systems and computer operations. Each digit in a binary number is called a bit, and each bit represents a power of 2.

Gray Code: Gray code, also known as reflected binary code, is a binary numeral system where adjacent values differ by only one bit. It is commonly used in various applications such as analog-to-digital converters, error detection, and rotary encoders. The advantage of Gray code is that it prevents errors caused by multiple bits changing simultaneously during transitions.

Problem Statement

Write a C program that converts a binary number to its equivalent Gray code using recursion. The program should prompt the user to enter a binary number and display the corresponding Gray code.

Input:

• An unsigned integer representing a binary number.

Output:

• The corresponding Gray code as an unsigned integer.

Example:

Enter a binary number: 1010

Gray code: 1111

Note:

• The input binary number is assumed to be a 32-bit unsigned integer.
• The program should use a recursive function to convert the binary number to Gray code.
• The program should handle invalid inputs appropriately and display error messages if necessary.

C Program to Convert Binary to Gray Code using Recursion

#include <stdio.h>

// Function to convert binary to Gray code
unsigned int binaryToGray(unsigned int num)
{
    if (num == 0)
        return 0;

    unsigned int msb = num & (1 << 31); // Extract the most significant bit

    // Right shift one position and XOR with the original number
    return (msb | (num >> 1)) ^ binaryToGray(num >> 1);
}

int main()
{
    unsigned int binaryNum;

    printf("Enter a binary number: ");
    scanf("%u", &binaryNum);

    unsigned int grayNum = binaryToGray(binaryNum);

    printf("Gray code: %u\n", grayNum);

    return 0;
}

How it Works

1. The program starts by including the necessary header file stdio.h for input/output operations.
2. The function binaryToGray is declared. This function takes an unsigned integer num as input and returns the Gray code for that number.
3. Inside the binaryToGray function, the following steps are performed recursively:
   • Base Case: If the number is 0, meaning there are no more bits to process, the function returns 0, as the Gray code for 0 is also 0.
   • The most significant bit (MSB) of the number is extracted using the bitwise AND operation with (1 << 31). This operation isolates the leftmost bit of the 32-bit number.
   • The number is then right-shifted by one position to discard the MSB. This is done using the right shift operator >>.
   • The function makes a recursive call to itself with the remaining bits of the number (after discarding the MSB).
   • The result obtained from the recursive call is XORed with the MSB. This is done to ensure that adjacent values in the Gray code differ by only one bit.
   • The final result is returned.
4. In the main function:
   • The program prompts the user to enter a binary number and reads it as an unsigned integer using scanf.
   • The binaryToGray function is called with the input binary number as an argument, and the result is stored in the grayNum variable.
   • Finally, the program prints the calculated Gray code using printf.
5. The program terminates by returning 0 from the main function.

The recursion in the binaryToGray function processes the bits of the binary number one by one, starting from the most significant bit (MSB) and moving towards the least significant bit (LSB). At each recursive step, the function extracts the MSB, discards it, and processes the remaining bits recursively. The process continues until the base case is reached (num == 0), and the Gray code is constructed by XORing the extracted MSB with the result obtained from the recursive call.

Input /Output

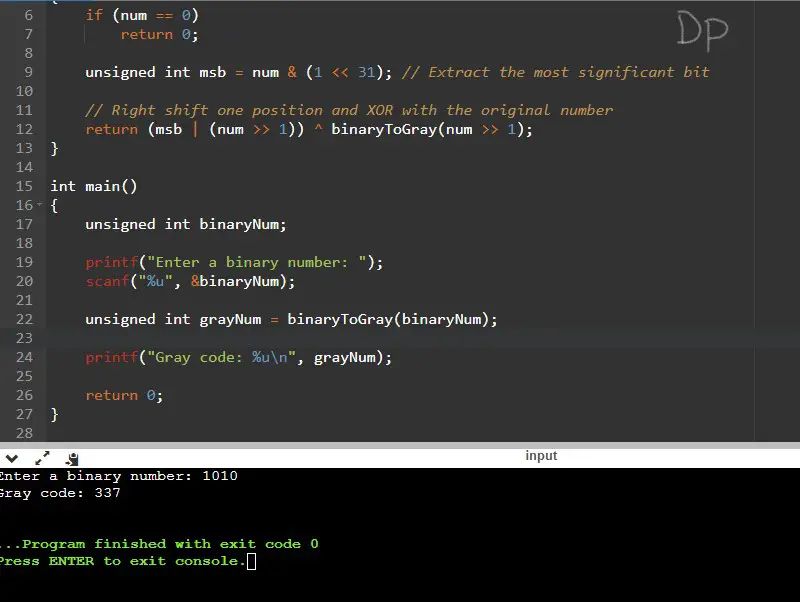
Explanation:

• The program prompts the user to enter a binary number.
• The user enters the binary number 1010.
• The binaryToGray function is called with the input number 1010.
  • Since 1010 is not equal to 0, the function proceeds with the recursion.
  • The most significant bit (MSB) is extracted, which is 1.
  • The number is right-shifted by one position, resulting in 0101.
  • The function makes a recursive call to binaryToGray with the remaining bits 0101.
    • Again, the number is not equal to 0, so the recursion continues.
    • The MSB is extracted, which is 0.
    • The number is right-shifted by one position, resulting in 0010.
    • Another recursive call is made with the remaining bits 0010.
      • The number is still not equal to 0, so the recursion continues.
      • The MSB is extracted, which is 0.
      • The number is right-shifted by one position, resulting in 0001.
      • Another recursive call is made with the remaining bits 0001.
        • The number is not equal to 0, so the recursion continues.
        • The MSB is extracted, which is 0.
        • The number is right-shifted by one position, resulting in 0000.
        • Another recursive call is made with the remaining bits 0000.
          • The number is now equal to 0, so the base case is reached.
          • The function returns 0.
      • The result of the recursive call is XORed with the MSB 0, resulting in 0.
      • The function returns 0.
    • The result of the recursive call is XORed with the MSB 0, resulting in 0.
    • The function returns 0.
  • The result of the recursive call is XORed with the MSB 1, resulting in 1.
  • The function returns 1.
• The calculated Gray code 337 is printed as the output.

In this example, the binary number 1010 is converted to its equivalent Gray code 337 using the recursive approach implemented in the program.