Python Program to Print All Permutations of a String in Lexicographic Order using Recursion

In this Python program, we embark on an exploration of permutations and lexicographic ordering. We will employ the power of recursion to generate and display all permutations of a given string in lexicographic order. Recursion, a programming technique where a function calls itself, is well-suited for solving such problems, as it naturally mirrors the recursive nature of permutations.

Problem Statement

You are tasked with writing a Python program that generates and prints all permutations of a given string in lexicographic order using recursion.

Python Program to Print All Permutations of a String in Lexicographic Order using Recursion

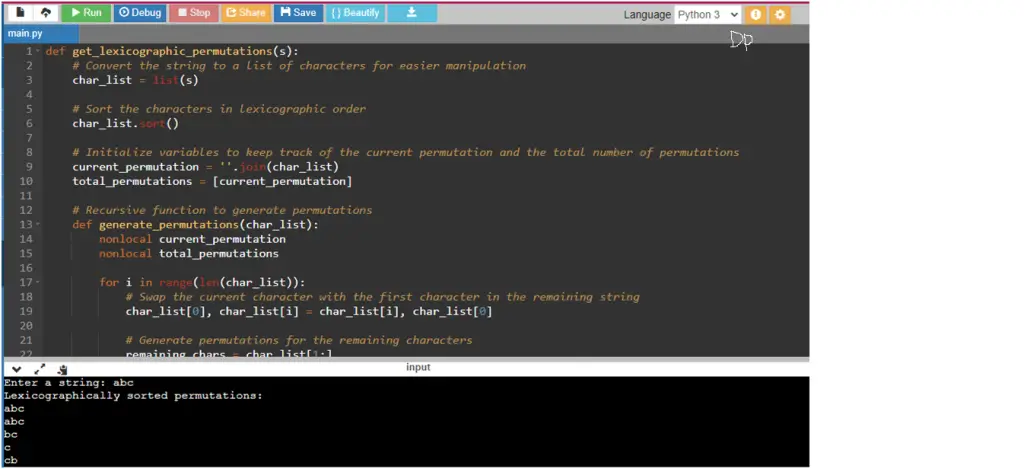
def get_lexicographic_permutations(s):
    # Convert the string to a list of characters for easier manipulation
    char_list = list(s)
    
    # Sort the characters in lexicographic order
    char_list.sort()
    
    # Initialize variables to keep track of the current permutation and the total number of permutations
    current_permutation = ''.join(char_list)
    total_permutations = [current_permutation]
    
    # Recursive function to generate permutations
    def generate_permutations(char_list):
        nonlocal current_permutation
        nonlocal total_permutations

        for i in range(len(char_list)):
            # Swap the current character with the first character in the remaining string
            char_list[0], char_list[i] = char_list[i], char_list[0]

            # Generate permutations for the remaining characters
            remaining_chars = char_list[1:]
            remaining_chars.sort()  # Sort the remaining characters
            current_permutation = char_list[0] + ''.join(remaining_chars)

            # Add the current permutation to the list of permutations
            total_permutations.append(current_permutation)

            # Recursively generate permutations for the remaining characters
            generate_permutations(remaining_chars)

            # Restore the original order of characters for backtracking
            char_list[0], char_list[i] = char_list[i], char_list[0]

   generate_permutations(char_list)
    
    return total_permutations

# Input a string
input_string = input("Enter a string: ")

# Get and print lexicographically sorted permutations
permutations = get_lexicographic_permutations(input_string)
print("Lexicographically sorted permutations:")
for permutation in permutations:
    print(permutation)

How it works

To generate all permutations of a string in lexicographic order using recursion, we’ll break down the problem into smaller, manageable steps. Here’s how the program works step by step:

1. Input: The program starts by taking a single input, which is the string for which we want to generate permutations.
2. Convert to List: We convert the input string into a list of characters. This list will make it easier to manipulate the characters during the permutation generation process.
3. Sort Characters: We sort the characters in the list in lexicographic order. This is done to ensure that we generate permutations in lexicographic order.
4. Initialization: We initialize a list, total_permutations, to store all permutations, and a variable, current_permutation, to store the current permutation being generated. Initially, current_permutation is set to the sorted input string.
5. Recursive Function: We define a recursive function, generate_permutations(char_list), that takes the list of characters as an argument. This function generates permutations recursively.
6. Base Case: The base case of the recursion is when there’s only one character left in char_list. At this point, we’ve generated a permutation, so we add current_permutation to the list of total_permutations.
7. Permutation Generation:
   • We iterate through the characters in char_list, and for each character:
   • We swap it with the first character in char_list.
   • We generate permutations for the remaining characters (excluding the first character), which are stored in remaining_chars.
   • We sort remaining_chars to ensure they are in lexicographic order.
   • We update current_permutation with the first character followed by remaining_chars.
   • We add current_permutation to the list of total_permutations.
   • We make a recursive call to generate_permutations with the remaining_chars.
   • After the recursive call, we restore the original order of characters by swapping them back.
8. Generate Permutations: We call the generate_permutations function with the sorted list of characters, which starts the recursive process of generating all permutations.
9. Output: Finally, we print the total_permutations list, which contains all permutations of the input string in lexicographic order.

The recursion ensures that all possible combinations of characters are explored, leading to the generation of all permutations. Sorting the characters and carefully manipulating them during the recursion guarantees that the permutations are produced in lexicographic order.

Input/Output