Python Program to Implement Comb Sort

Comb Sort is a relatively simple sorting algorithm that improves upon the performance of Bubble Sort. It was designed to address some of the limitations of Bubble Sort while maintaining its intuitive nature. Comb Sort was introduced by Włodzimierz Dobosiewicz in 1980.

Problem Statement

You are given an unsorted array of integers. Your task is to implement the Comb Sort algorithm in Python to sort the array in non-decreasing order.

Python Program to Implement Comb Sort

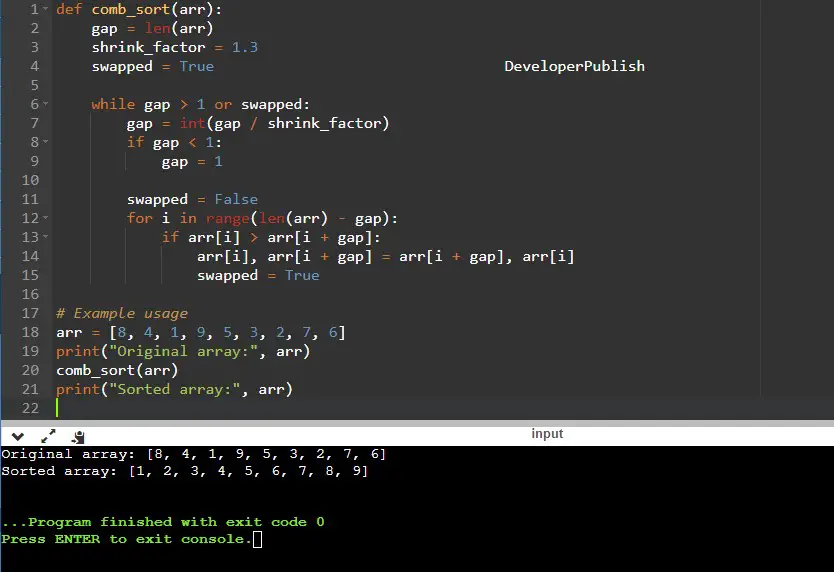
def comb_sort(arr):
    gap = len(arr)
    shrink_factor = 1.3
    swapped = True
    
    while gap > 1 or swapped:
        gap = int(gap / shrink_factor)
        if gap < 1:
            gap = 1
        
        swapped = False
        for i in range(len(arr) - gap):
            if arr[i] > arr[i + gap]:
                arr[i], arr[i + gap] = arr[i + gap], arr[i]
                swapped = True

# Example usage
arr = [8, 4, 1, 9, 5, 3, 2, 7, 6]
print("Original array:", arr)
comb_sort(arr)
print("Sorted array:", arr)

How it Works

1. Initialization:
   • Start with an initial gap value, usually set to the length of the array.
   • Initialize a boolean variable swapped as True. This will be used to check if any swaps are made in a pass.
2. Main Loop:
   • Enter a loop that continues until the gap becomes 1 and no swaps are made in a pass.
   • Calculate the new gap using a reduction factor. A common choice is a factor of around 1.3.
3. Comparing and Swapping:
   • Iterate through the array from index 0 to (array_length - gap).
   • Compare elements that are gap positions apart. If the element at index i is greater than the element at index i + gap, swap them.
   • Set swapped to True if any swaps are made during this iteration.
4. Updating the Gap:
   • After comparing and swapping elements with the current gap, reduce the gap size.
   • Continue the loop with the updated gap.
5. Final Pass:
   • When the gap becomes 1, continue the loop for one final pass using a gap of 1.
   • Perform a regular Bubble Sort within this pass to ensure that any remaining smaller elements are moved to their correct positions.
6. Termination:
   • Exit the main loop when the gap becomes 1 and no swaps are made (swapped remains False).

The idea of gradually reducing the gap helps to quickly eliminate larger values from the end of the array, as larger values tend to move more slowly in Bubble Sort-like algorithms. By the time the gap becomes 1, the array is nearly sorted, and a final pass with a gap of 1 ensures that any remaining elements are properly ordered.

It’s important to note that while Comb Sort is more efficient than Bubble Sort on average cases, it’s still not as efficient as some other sorting algorithms like Quick Sort or Merge Sort. However, its simplicity and ease of implementation make it an interesting algorithm to study and understand.

Input/ Output