C Program to Find Determinant of a Matrix
This C program calculates the determinant of a square matrix provided by the user.
Problem statement
Given a square matrix (same number of rows and columns), we need to find its determinant. The program prompts the user to enter the elements of the matrix and then calculates and displays the determinant.
C Program to Find Determinant of a Matrix
#include <stdio.h>
#define N 10 // Maximum matrix size
// Function to calculate the determinant of a matrix
double determinant(double matrix[N][N], int size) {
double det = 0;
double submatrix[N][N];
if (size == 2) {
return ((matrix[0][0] * matrix[1][1]) - (matrix[1][0] * matrix[0][1]));
} else {
for (int x = 0; x < size; x++) {
int subi = 0;
for (int i = 1; i < size; i++) {
int subj = 0;
for (int j = 0; j < size; j++) {
if (j == x)
continue;
submatrix[subi][subj] = matrix[i][j];
subj++;
}
subi++;
}
det += (x % 2 == 0 ? 1 : -1) * matrix[0][x] * determinant(submatrix, size - 1);
}
}
return det;
}
int main() {
int size;
double matrix[N][N];
printf("Enter the size of the square matrix (max %d): ", N);
scanf("%d", &size);
if (size <= 0 || size > N) {
printf("Invalid matrix size. Please enter a valid size.\n");
return 1;
}
printf("Enter the elements of the matrix:\n");
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
scanf("%lf", &matrix[i][j]);
}
}
double det = determinant(matrix, size);
printf("The determinant of the matrix is: %.2lf\n", det);
return 0;
}
How it works
- The program begins with the inclusion of the necessary header file,
stdio.h, which provides input/output functionality. - The maximum matrix size is defined using the
#definedirective. In this program, it is set to 10 as#define N 10. - The
determinantfunction is declared, which is responsible for calculating the determinant of the matrix. It takes two parameters: the matrix itself, represented as a 2D arraydouble matrix[N][N], and the size of the matrix. - Inside the
determinantfunction, there is a base case that checks if the size of the matrix is 2. If so, it directly calculates and returns the determinant of the 2×2 matrix using the formula((a * d) - (b * c)). - If the size is greater than 2, the function proceeds to calculate the determinant recursively using the Laplace expansion method.
- A nested loop is used to iterate over each element in the first row of the matrix. For each element, a submatrix is created by excluding the current row and column.
- The submatrix is then populated with the appropriate elements from the original matrix, and the
determinantfunction is recursively called with the submatrix and a reduced size (size – 1). - The determinant of the submatrix is multiplied by the corresponding element in the first row of the original matrix, and the sign of the product alternates based on the position of the element (even or odd).
- The calculated products are accumulated to obtain the final determinant of the matrix.
- The
mainfunction is implemented, which is the entry point of the program. - The user is prompted to enter the size of the square matrix, and the value is stored in the
sizevariable usingscanf. - Input validation is performed to ensure that the matrix size is within the defined limits. If the size is invalid, an error message is displayed, and the program exits with a non-zero status code.
- The user is then prompted to enter the elements of the matrix. Two nested loops are used to iterate over each element, and the values are stored in the
matrixarray. - The
determinantfunction is called with the matrix and size as arguments, and the result is stored in thedetvariable. - Finally, the calculated determinant is displayed to the user using
printf.
That’s how the program works! It calculates the determinant of a square matrix by implementing the Laplace expansion method recursively.
Input / Output
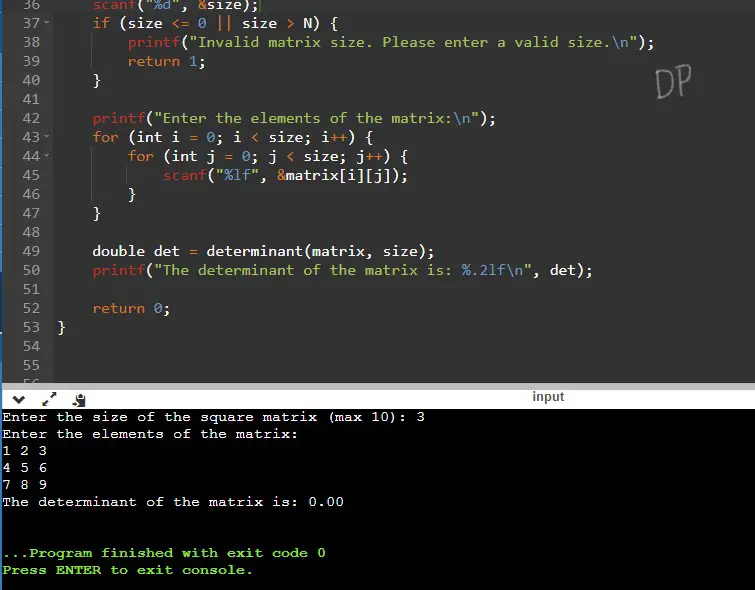

Leave a Review