C Program to Evaluate the Given Polynomial Equation

This C program evaluates a polynomial equation for a given value of x.

Problem Statement

Write a C program to Evaluate the Given Polynomial Equation.

The polynomial equation is of the form:

P(x) = a_n * x^n + a_(n-1) * x^(n-1) + … + a_1 * x + a_0

where P(x) represents the polynomial equation, a_n to a_0 are the coefficients of each term, and n is the degree of the polynomial.

The program should perform the following steps:

1. Prompt the user to enter the degree of the polynomial equation.
2. Allocate memory for an array to store the coefficients based on the degree.
3. Prompt the user to enter the coefficients for each term of the polynomial equation.
4. Prompt the user to enter a value for x.
5. Compute the result of the polynomial equation using Horner’s method.
6. Display the result on the screen.

Note:

• Assume that the user will enter valid inputs.
• Use double data type to handle decimal coefficients and values of x.
• Handle the case where the degree of the polynomial equation is zero (constant term only).

C Program to Evaluate the Given Polynomial Equation

#include <stdio.h>
#include <stdlib.h>

// Function to evaluate the polynomial equation using Horner's method
double evaluatePolynomial(double x, double coefficients[], int degree) {
    double result = coefficients[degree];
    
    for (int i = degree - 1; i >= 0; i--) {
        result = result * x + coefficients[i];
    }
    
    return result;
}

int main() {
    int degree;
    double x;
    
    printf("Enter the degree of the polynomial equation: ");
    scanf("%d", &degree);
    
    // Allocate memory for coefficients
    double* coefficients = (double*)malloc((degree + 1) * sizeof(double));
    
    printf("Enter the coefficients of the polynomial equation:\n");
    for (int i = degree; i >= 0; i--) {
        printf("Coefficient of x^%d: ", i);
        scanf("%lf", &coefficients[i]);
    }
    
    printf("Enter the value of x: ");
    scanf("%lf", &x);
    
    // Evaluate the polynomial equation
    double result = evaluatePolynomial(x, coefficients, degree);
    
    printf("The result of the polynomial equation for x = %.2lf is %.2lf\n", x, result);
    
    // Free allocated memory
    free(coefficients);
    
    return 0;
}

How it Works

1. The program starts by prompting the user to enter the degree of the polynomial equation. This value determines the size of the coefficients array.
2. Memory is dynamically allocated for the coefficients array using the malloc function. The size of the array is (degree + 1) since it needs to store coefficients from degree n down to degree 0.
3. The program then prompts the user to enter the coefficients for each term of the polynomial equation. It uses a loop to iterate from the highest degree to the constant term (i starts from degree and goes down to 0).
4. Inside the loop, the program asks the user for the coefficient of x^i and stores it in the corresponding index of the coefficients array.
5. After all the coefficients are entered, the program asks the user to enter a value for x.
6. The program calls the evaluatePolynomial function, passing the value of x, the coefficients array, and the degree of the polynomial equation. This function evaluates the polynomial using Horner’s method.
7. In the evaluatePolynomial function, the result is initialized with the coefficient of the highest degree term (coefficients[degree]).
8. Using a loop, the function iterates from the second highest degree term down to the constant term. It multiplies the current result by x and adds the next coefficient to it, following Horner’s method.
9. The final result of the polynomial equation is returned from the evaluatePolynomial function.
10. Back in the main function, the result is stored in the result variable.
11. Finally, the program displays the result on the screen using printf.
12. The memory allocated for the coefficients array is freed using the free function to release the allocated memory.

That’s how the program works! It dynamically allocates memory for the coefficients array, evaluates the polynomial equation using Horner’s method, and displays the result to the user.

Input / Output

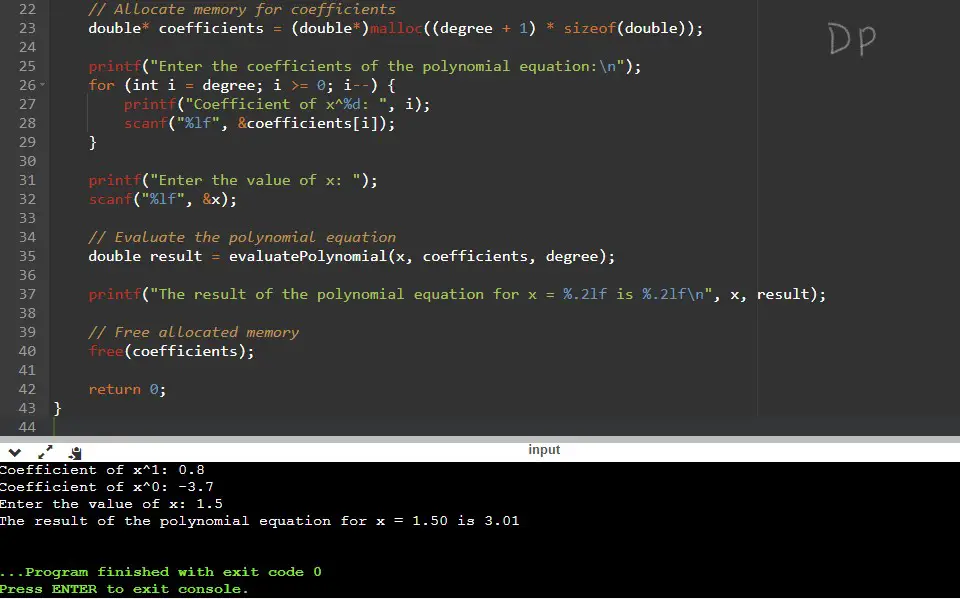
Explanation:

In this example, the user is asked to enter the degree of the polynomial equation, which is 3. The program dynamically allocates memory for an array of size 4 (degree + 1).

Next, the user is prompted to enter the coefficients for each term of the polynomial equation. They enter the coefficients as 2.5, -1.3, 0.8, and -3.7 for x^3, x^2, x^1, and x^0 terms, respectively.

The program then asks the user to enter the value of x, and they enter 1.5.

The program calls the evaluatePolynomial function, passing the value of x, the coefficients array, and the degree.

The evaluatePolynomial function uses Horner’s method to evaluate the polynomial equation: 2.5 * 1.5^3 - 1.3 * 1.5^2 + 0.8 * 1.5 - 3.7. It computes the result and returns -5.85.

Finally, the program displays the result: “The result of the polynomial equation for x = 1.50 is 3.01”.

That’s how the input and output of the program work! The user provides the degree and coefficients of the polynomial equation, as well as the value of x, and the program calculates and displays the result of the equation.