C Program demonstrating Tower of Hanoi

The Tower of Hanoi is a classic mathematical puzzle that involves moving a stack of disks from one peg to another, following a specific set of rules. It is often used as an example in computer science and programming courses to demonstrate recursion.

The puzzle consists of three pegs and a number of disks of different sizes, which can be stacked in ascending order of size on one of the pegs.

The Tower of Hanoi problem can be solved using a recursive algorithm. The recursive approach breaks down the problem into smaller subproblems, making use of the fact that the larger disks act as a temporary storage for the smaller disks during the move.

The general recursive algorithm for solving the Tower of Hanoi problem is as follows:

1. If there is only one disk, move it from the source peg to the destination peg directly.
2. Otherwise, recursively move n-1 disks from the source peg to the auxiliary peg, using the destination peg as the auxiliary.
3. Move the largest disk from the source peg to the destination peg.
4. Recursively move the n-1 disks from the auxiliary peg to the destination peg, using the source peg as the auxiliary.

By following these steps recursively, the program can determine the exact sequence of moves required to solve the Tower of Hanoi problem for any given number of disks.

Implementing and understanding the Tower of Hanoi problem helps in grasping the concept of recursion and its applications in solving complex problems efficiently.

Problem statement

The Tower of Hanoi problem can be stated as follows:

Given three pegs (A, B, and C) and a set of disks of different sizes, initially stacked in ascending order of size on one peg (let’s say peg A), the objective is to transfer the entire stack of disks to another peg (let’s say peg C). However, the following rules must be followed:

1. Only one disk can be moved at a time.
2. At no point can a larger disk be placed on top of a smaller disk.

The task is to devise an algorithm that determines the optimal sequence of moves to solve the Tower of Hanoi problem for a given number of disks. The algorithm should minimize the number of moves required to complete the puzzle, while adhering to the rules mentioned above.

The challenge lies in developing a recursive solution that breaks down the problem into smaller subproblems, utilizing the concept of auxiliary pegs to facilitate the movement of the disks. The goal is to find an efficient way to transfer all the disks from the source peg to the destination peg, ensuring that the rules are followed throughout the process.

Solving the Tower of Hanoi problem requires logical reasoning, an understanding of recursive algorithms, and the ability to devise a step-by-step strategy to solve complex problems. It serves as an excellent exercise for developing problem-solving skills and gaining familiarity with recursive thinking.

C Program demonstrating Tower of Hanoi

#include <stdio.h>

void towerOfHanoi(int n, char source, char destination, char auxiliary) {
    if (n == 1) {
        printf("Move disk 1 from %c to %c\n", source, destination);
        return;
    }
    towerOfHanoi(n - 1, source, auxiliary, destination);
    printf("Move disk %d from %c to %c\n", n, source, destination);
    towerOfHanoi(n - 1, auxiliary, destination, source);
}

int main() {
    int n;
    printf("Enter the number of disks: ");
    scanf("%d", &n);
    printf("Steps to solve the Tower of Hanoi problem:\n");
    towerOfHanoi(n, 'A', 'C', 'B');
    return 0;
}

How it Works

The Tower of Hanoi problem is solved using a recursive algorithm. The recursive approach breaks down the problem into smaller subproblems, making use of the fact that the larger disks act as temporary storage for the smaller disks during the move. Here’s how the algorithm works:

1. The Tower of Hanoi function is called with the following parameters:
   • n: The number of disks to be moved.
   • source: The name of the source peg.
   • destination: The name of the destination peg.
   • auxiliary: The name of the auxiliary peg.
2. If n is equal to 1, it means there is only one disk to move. In this case, the function simply prints the move from the source peg to the destination peg.
3. If n is greater than 1, the function follows these steps:
   • Step 1: Recursively move n-1 disks from the source peg to the auxiliary peg, using the destination peg as the auxiliary. This step is accomplished by calling the Tower of Hanoi function itself, but with n-1 disks and with the destination peg as the auxiliary peg.
   • Step 2: Print the move of the largest disk from the source peg to the destination peg.
   • Step 3: Recursively move the n-1 disks from the auxiliary peg to the destination peg, using the source peg as the auxiliary. Again, this step is accomplished by calling the Tower of Hanoi function with n-1 disks, but with the source peg as the auxiliary peg.
4. The recursion continues until n becomes 1, at which point the moves are printed directly, and the function returns.

By following this recursive algorithm, the Tower of Hanoi problem can be solved for any given number of disks. The recursion ensures that each disk is moved to the desired position while maintaining the rules of the puzzle. The larger disks act as temporary storage areas to facilitate the movement of the smaller disks, ultimately achieving the goal of transferring the entire stack from the source peg to the destination peg.

Input / Output

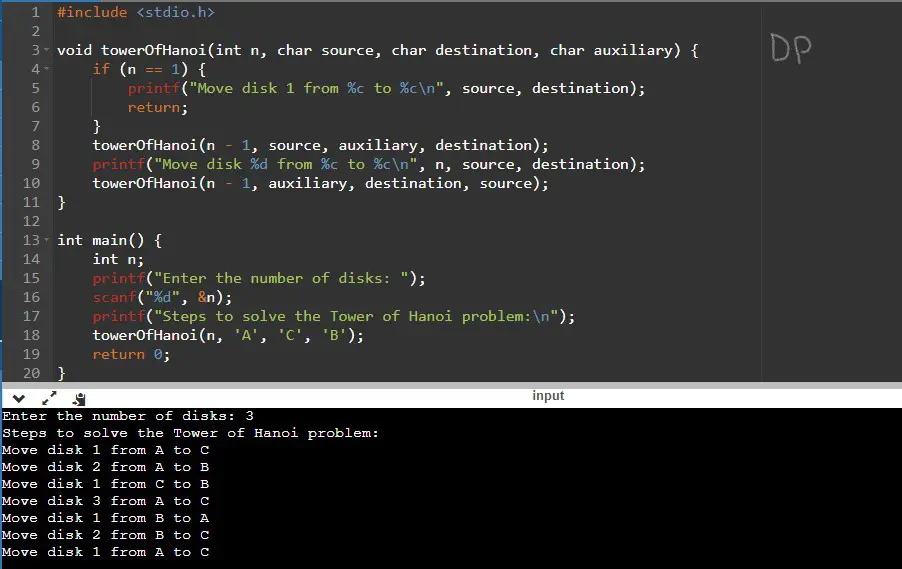
The program will prompt you to enter the number of disks. In this case, we enter 3. Then, it will print each step required to solve the Tower of Hanoi problem, indicating the disk number and the move from one peg to another.

Note: The letters A, B, and C represent the three pegs (source, auxiliary, and destination).