Python Program to Implement Queue using Linked List

A queue is a linear data structure that follows the First-In-First-Out (FIFO) principle, which means that the element added to the queue first will be the first one to be removed. Queues are used in situations where tasks or data must be processed in the order they are received.

Problem Statement

You need to implement a queue data structure using a singly linked list using python.

Python Program to Implement Queue using Linked List

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class QueueLinkedList:
    def __init__(self):
        self.front = None
        self.rear = None

    def is_empty(self):
        return self.front is None

    def enqueue(self, data):
        new_node = Node(data)
        if self.rear is None:
            self.front = new_node
            self.rear = new_node
        else:
            self.rear.next = new_node
            self.rear = new_node

    def dequeue(self):
        if self.is_empty():
            print("Queue is empty")
            return None
        else:
            dequeued_item = self.front.data
            self.front = self.front.next
            if self.front is None:
                self.rear = None
            return dequeued_item

    def peek(self):
        if self.is_empty():
            print("Queue is empty")
            return None
        else:
            return self.front.data

    def display(self):
        current = self.front
        while current:
            print(current.data, end=" ")
            current = current.next
        print()

# Creating a queue and performing operations
queue = QueueLinkedList()
queue.enqueue(10)
queue.enqueue(20)
queue.enqueue(30)

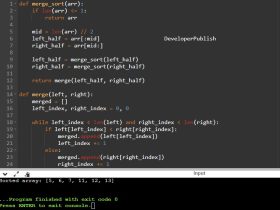
print("Queue:")
queue.display()

print("Peek:", queue.peek())

print("Dequeue:", queue.dequeue())
print("Dequeue:", queue.dequeue())

print("Queue after dequeuing:")
queue.display()

How it Works

1. Define the Node Class: The first step is to define a Node class that represents individual elements in the linked list. Each node contains two parts:

• data: The actual value stored in the node (in this case, the element of the queue).
• next: A reference to the next node in the linked list.

2. Define the Queue Linked List Class: Next, you define the main class that will manage the queue operations using the linked list. This class will have two pointers: front and rear, which point to the first and last nodes of the linked list, respectively.

3. Enqueue Operation: The enqueue operation adds an element to the rear of the queue (end of the linked list). Here’s how it works:

• Create a new node with the provided data.
• If the queue is empty (both front and rear are None), set both front and rear to the new node.
• Otherwise, update the next reference of the current rear node to point to the new node, and then update the rear pointer to the new node.

4. Dequeue Operation: The dequeue operation removes and returns the element from the front of the queue. Here’s how it works:

• If the queue is empty (both front and rear are None), return an appropriate message.
• Otherwise, store the data of the current front node, update the front pointer to the next node, and if the new front is None, update the rear pointer as well.
• Return the stored data.

5. Peek Operation: The peek operation returns the element at the front of the queue without removing it. It’s similar to the dequeue operation, but without modifying the pointers.

6. Display and is_empty Operations: The display operation traverses the linked list and prints the elements of the queue. The is_empty operation checks if the queue is empty based on the front pointer.

Input/ Output