Python Program to Implement Heap Sort

Heap Sort is a popular comparison-based sorting algorithm that uses a binary heap data structure to efficiently organize and sort elements in an array. It falls under the category of “comparison-based” sorting algorithms, meaning it compares elements in the array and swaps them if needed to achieve the desired order. Heap Sort is known for its time complexity and is often used in various programming scenarios.

Problem Statement

You are given an unsorted array of integers. Your task is to implement the Heap Sort algorithm in Python to sort the array in ascending order.

Python Program to Implement Heap Sort

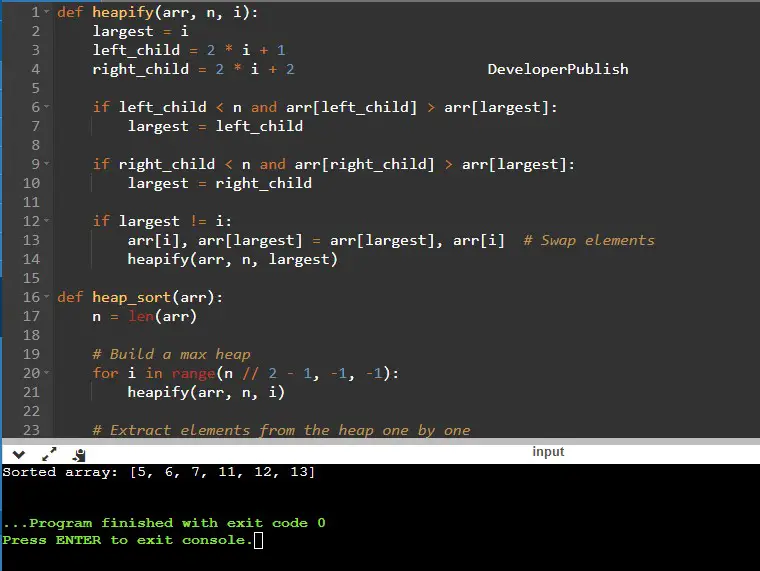
def heapify(arr, n, i):
    largest = i
    left_child = 2 * i + 1
    right_child = 2 * i + 2
    
    if left_child < n and arr[left_child] > arr[largest]:
        largest = left_child
    
    if right_child < n and arr[right_child] > arr[largest]:
        largest = right_child
    
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # Swap elements
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)
    
    # Build a max heap
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)
    
    # Extract elements from the heap one by one
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # Swap elements
        heapify(arr, i, 0)

# Example usage
arr = [12, 11, 13, 5, 6, 7]
heap_sort(arr)
print("Sorted array:", arr)

How it Works

1. Building the Max Heap: The first step is to build a max heap from the given array. This involves rearranging the array’s elements to satisfy the max heap property. To achieve this, we start from the last non-leaf node in the array (at index n // 2 - 1) and perform a process called “heapify” on each node. Heapify ensures that the largest element among the node and its children is moved to the node’s position.The heapify process involves comparing the element at the current node with its left and right children. If either child is larger than the current node, a swap is performed. After the swap, the process is recursively applied to the affected subtree to ensure the max heap property is maintained.
2. Sorting: Once the max heap is constructed, the largest element is at the root of the heap (index 0). The main sorting process involves repeatedly swapping the root element with the last element of the heap (which corresponds to the end of the unsorted portion of the array), reducing the heap size by one, and then heapifying the new root to maintain the max heap property.The effect of this process is that the largest element “bubbles down” to its correct position in the sorted section of the array, while the heap property is maintained for the remaining elements. This step is repeated until the entire array is sorted.

Here’s a more detailed breakdown of the sorting process:

• Swap the root element (largest) with the last element in the heap (end of unsorted section).
• Reduce the heap size by one (effectively removing the sorted element from the heap).
• Heapify the root to ensure the max heap property is maintained.

Repeat these steps until the heap size becomes 1, meaning all elements have been moved from the heap to the sorted section of the array.

It’s important to note that Heap Sort doesn’t require extra space proportional to the input array’s size like Merge Sort does, making it more memory-efficient in some cases. However, it’s not as cache-friendly as some other sorting algorithms, which might affect its performance for smaller arrays or certain hardware configurations.

Input/ Output