Python Program to Implement Depth First Search on a Graph using Recursion

This Python program implements Depth-First Search (DFS) on a graph using recursion. DFS explores as far as possible along each branch before backtracking.

Depth First Search (DFS) is a graph traversal algorithm that explores as far as possible along a branch before backtracking. It’s often implemented using recursion or a stack data structure. DFS is used to explore and analyze graphs, find connected components, solve puzzles, and more. In this introduction, I’ll provide an overview of how to implement DFS on a graph using recursion.

Problem Statement

You are given a graph represented as an adjacency list. Implement the Depth First Search (DFS) algorithm using recursion to traverse the graph, starting from a given source vertex. Your task is to print the vertices in the order they are visited during the DFS traversal.

Python Program to Implement Depth First Search on a Graph using Recursion

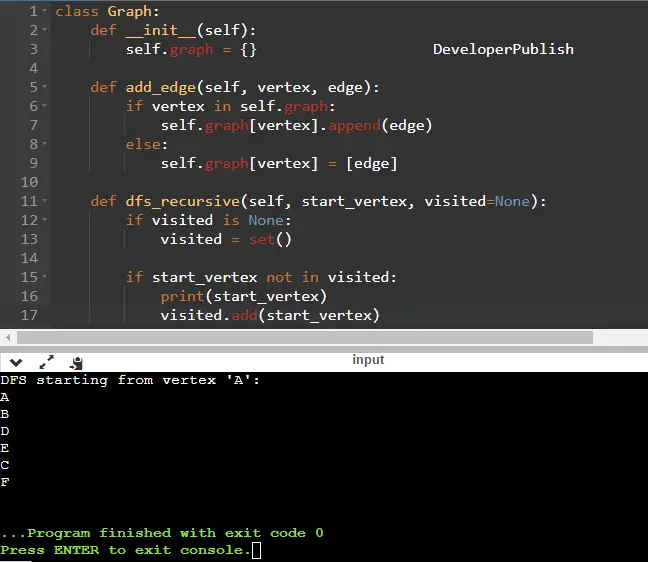
class Graph:
    def __init__(self):
        self.graph = {}

    def add_edge(self, vertex, edge):
        if vertex in self.graph:
            self.graph[vertex].append(edge)
        else:
            self.graph[vertex] = [edge]

    def dfs_recursive(self, start_vertex, visited=None):
        if visited is None:
            visited = set()
        
        if start_vertex not in visited:
            print(start_vertex)
            visited.add(start_vertex)

            if start_vertex in self.graph:
                for neighbor in self.graph[start_vertex]:
                    self.dfs_recursive(neighbor, visited)

# Create a graph and add edges
g = Graph()
g.add_edge('A', 'B')
g.add_edge('A', 'C')
g.add_edge('B', 'D')
g.add_edge('B', 'E')
g.add_edge('C', 'F')

# Perform DFS starting from vertex 'A'
print("DFS starting from vertex 'A':")
g.dfs_recursive('A')

How it Works

1. Initialization:
   • Create an empty set or list to keep track of visited vertices. We’ll use a set called visited.
2. Starting Vertex:
   • Begin the DFS traversal from the given source vertex. Mark this vertex as visited by adding it to the visited set.
3. Recursive Exploration:
   • For the current vertex, explore all of its unvisited neighboring vertices.
   • For each unvisited neighbor:
     • Mark the neighbor as visited by adding it to the visited set.
     • Recursively apply the DFS algorithm to the unvisited neighbor. This step effectively explores deeper into the graph along the current branch.
   • Repeat this process for all unvisited neighbors of the current vertex.
4. Backtracking:
   • When there are no unvisited neighbors left for the current vertex, return from the recursion. This represents backtracking to the previous level in the graph traversal.
   • Continue this process until you have visited all reachable vertices from the source vertex.
5. Result:
   • During the DFS traversal, the algorithm will print the vertices in the order they are visited. This order forms a depth-first traversal of the graph, where you explore as far as possible along one branch before backtracking.

Input/ Output