Python Program to Implement Bubble Sort

Bubble Sort is a simple and straightforward sorting algorithm used to arrange elements in a list or array into a particular order. It belongs to the class of comparison-based sorting algorithms, where elements are compared with each other to determine their relative order and then appropriately rearranged.

Problem Statement

You are given an unsorted list of integers. Your task is to implement the Bubble Sort algorithm in python to sort the list in ascending order.

Python Program to Implement Bubble Sort

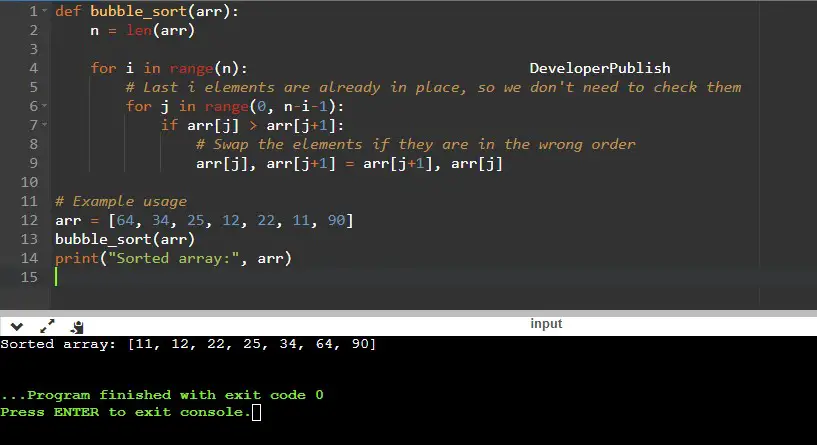
def bubble_sort(arr):
    n = len(arr)
    
    for i in range(n):
        # Last i elements are already in place, so we don't need to check them
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                # Swap the elements if they are in the wrong order
                arr[j], arr[j+1] = arr[j+1], arr[j]

# Example usage
arr = [64, 34, 25, 12, 22, 11, 90]
bubble_sort(arr)
print("Sorted array:", arr)

How it Works

1. Initialization: Start by considering the first two elements of the list.
2. Comparison and Swapping: Compare the first element with the second element. If the first element is greater than the second element, swap them. Otherwise, leave them in their positions.
3. Pass through the List: Move to the next pair of elements (the second and third elements) and compare them. Again, if the second element is greater than the third element, swap them; otherwise, leave them as they are.
4. Complete Pass: Continue this process, comparing and swapping adjacent elements as necessary, until you reach the end of the list. This completes one pass through the list.
5. Multiple Passes: Repeat the entire process for multiple passes. After the first pass, the largest element will have “bubbled up” to the end of the list. After the second pass, the second-largest element will be in the second-to-last position, and so on.
6. Termination: Continue the passes until no more swaps are needed. This means that the entire list is sorted. If no swaps are performed in a pass, it indicates that the list is now in the correct order, and the algorithm can terminate.
7. Sorted Output: At the end of the algorithm, you will have a sorted list with the smallest element at the beginning and the largest element at the end.

Here’s a simple example to illustrate the steps:

Unsorted List: [5, 2, 9, 1, 5, 6]

• Pass 1: [2, 5, 1, 5, 6, 9]
• Pass 2: [2, 1, 5, 5, 6, 9]
• Pass 3: [1, 2, 5, 5, 6, 9]
• Pass 4: [1, 2, 5, 5, 6, 9]

After four passes, no swaps are needed, indicating that the list is sorted. The sorted list is [1, 2, 5, 5, 6, 9].

It’s important to note that while Bubble Sort is conceptually simple, its efficiency is relatively low compared to more advanced sorting algorithms, especially for large datasets. Each pass through the list requires potentially many comparisons and swaps, leading to a time complexity of O(n^2) in the worst case, where n is the number of elements in the list.

Input/ Output