Python Program to Find Minimum Spanning Tree using Prim’s Algorithm

This Python program finds the Minimum Spanning Tree (MST) of a weighted, connected graph using Prim’s algorithm. The MST is a subset of edges that connects all vertices with the minimum possible total edge weight.

Prim’s Algorithm is a greedy algorithm used in graph theory to find the Minimum Spanning Tree (MST) of a connected, weighted graph. A Minimum Spanning Tree of a graph is a subgraph that includes all the vertices of the original graph while minimizing the total weight or cost of the edges. It’s often used in various applications like network design, clustering, and optimization problems.

Problem Statement

Solve the Problem using the Minimum Spanning Tree (Prim’s Algorithm)

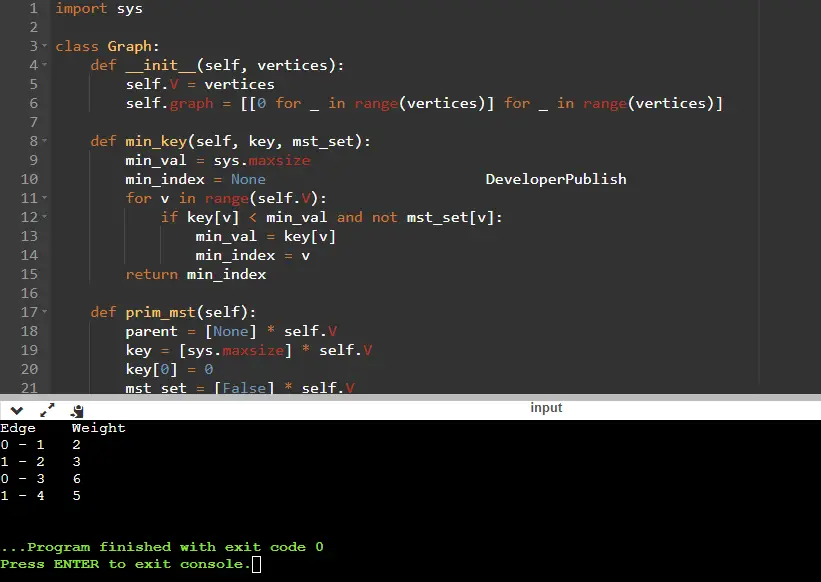
Python Program to Find Minimum Spanning Tree using Prim’s Algorithm

import sys

class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.graph = [[0 for _ in range(vertices)] for _ in range(vertices)]

    def min_key(self, key, mst_set):
        min_val = sys.maxsize
        min_index = None
        for v in range(self.V):
            if key[v] < min_val and not mst_set[v]:
                min_val = key[v]
                min_index = v
        return min_index

    def prim_mst(self):
        parent = [None] * self.V
        key = [sys.maxsize] * self.V
        key[0] = 0
        mst_set = [False] * self.V

        parent[0] = -1

        for _ in range(self.V):
            u = self.min_key(key, mst_set)
            mst_set[u] = True
            for v in range(self.V):
                if self.graph[u][v] and not mst_set[v] and key[v] > self.graph[u][v]:
                    key[v] = self.graph[u][v]
                    parent[v] = u

        self.print_mst(parent)

    def print_mst(self, parent):
        print("Edge \tWeight")
        for i in range(1, self.V):
            print(f"{parent[i]} - {i} \t{self.graph[i][parent[i]]}")


g = Graph(5)
g.graph = [[0, 2, 0, 6, 0],
           [2, 0, 3, 8, 5],
           [0, 3, 0, 0, 7],
           [6, 8, 0, 0, 9],
           [0, 5, 7, 9, 0]]

g.prim_mst()

How it Works

1. Initialization:
   • Choose an arbitrary starting vertex as the initial MST. This vertex is added to the MSTSet, a set that keeps track of vertices already included in the MST.
   • Initialize two data structures:
     • Key: A list or array that stores the minimum weight of edges connecting vertices in MSTSet to vertices outside it. Initially, set the Key value to infinity for all vertices except the starting vertex, which is set to 0.
     • Parent: A list or array that keeps track of the parent of each vertex in the MST. Initially, set the parent of all vertices to None.
2. Greedy Selection:
   • Find the vertex u that is not in MSTSet and has the minimum Key[u] value. This vertex u will be added to the MST next. The Key values effectively represent the weight of the shortest edge connecting each vertex outside the MST to a vertex in the MST.
3. Update Keys:
   • For each vertex v adjacent to u (i.e., connected by an edge), check if the weight of the edge u-v is less than the current Key[v]. If it is, update Key[v] with the weight of the edge u-v. This step ensures that you always select the minimum-weight edge to expand the MST.
4. Add Vertex to MST:
   • Add vertex u to the MSTSet. This means that u is now part of the Minimum Spanning Tree.
5. Repeat:
   • Repeat steps 2-4 until all vertices are included in the MSTSet. At this point, you’ve constructed the Minimum Spanning Tree. The Parent data structure will also allow you to reconstruct the tree’s edges.
6. Output:
   • The Minimum Spanning Tree consists of the edges that were selected during the algorithm. These edges form a connected subgraph with the minimum total weight among all possible spanning trees of the input graph.

Input/ Output