Python Program to Find Middle Element of a Linked List

This Python program finds the middle element of a singly linked list using the two-pointer technique. The middle element is the one that is halfway through the list.

Finding the middle element of a linked list is a common problem in computer programming and algorithmic interviews. The middle element of a linked list is the element that lies approximately in the middle of the list. If the list has an odd number of elements, there will be one exact middle element. If the list has an even number of elements, there could be two middle elements, but for simplicity, we often consider the one closer to the beginning of the list.

Problem Statement

Given a singly linked list, write a function to find the middle element of the list. If the list has an odd number of elements, return the exact middle element. If the list has an even number of elements, consider the one closer to the beginning of the list as the middle element.

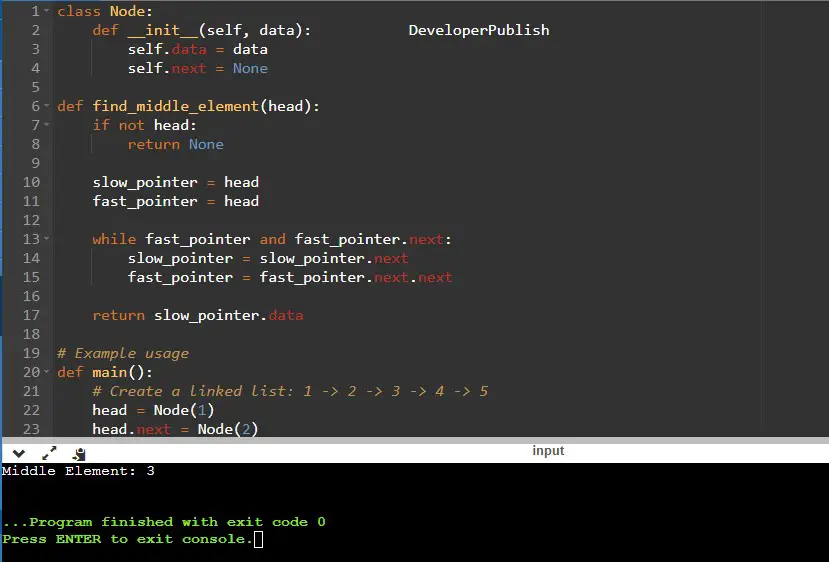
Python Program to Find Middle Element of a Linked List

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

def find_middle_element(head):
    if not head:
        return None

    slow_pointer = head
    fast_pointer = head

    while fast_pointer and fast_pointer.next:
        slow_pointer = slow_pointer.next
        fast_pointer = fast_pointer.next.next

    return slow_pointer.data

# Example usage
def main():
    # Create a linked list: 1 -> 2 -> 3 -> 4 -> 5
    head = Node(1)
    head.next = Node(2)
    head.next.next = Node(3)
    head.next.next.next = Node(4)
    head.next.next.next.next = Node(5)

    middle_element = find_middle_element(head)
    print("Middle Element:", middle_element)  # Output: Middle Element: 3

if __name__ == "__main__":
    main()

How it Works

1. Initialization:
   • We start with two pointers, the slow pointer (slow_pointer) and the fast pointer (fast_pointer), both initially pointing to the head of the linked list.
2. Traversal:
   • The fast pointer advances two steps at a time, and the slow pointer advances one step at a time.
   • This means that with each iteration, the fast pointer covers twice the distance as the slow pointer.
3. Finding the Middle:
   • As the fast pointer moves at twice the speed of the slow pointer, when the fast pointer reaches the end of the list (i.e., it becomes None or reaches the last node), the slow pointer will be approximately halfway through the list.
4. Returning the Middle Element:
   • Once the fast pointer reaches the end of the list, the slow pointer will be pointing to the middle element.
   • If the linked list has an odd number of elements, the slow pointer will be exactly at the middle element.
   • If the linked list has an even number of elements, the slow pointer will be pointing to the first middle element among the two.

Here’s a step-by-step breakdown of how the algorithm works for a linked list 1 -> 2 -> 3 -> 4 -> 5:

• Initial state: slow_pointer at 1, fast_pointer at 1
• After 1 iteration: slow_pointer at 2, fast_pointer at 3
• After 2 iterations: slow_pointer at 3, fast_pointer at 5
• After 3 iterations: slow_pointer at 4, fast_pointer at None (end of list)

The slow_pointer is pointing to the middle element, which is 3.

For a linked list with an even number of elements, like 1 -> 2 -> 3 -> 4 -> 5 -> 6, the algorithm will work similarly:

• After 1 iteration: slow_pointer at 2, fast_pointer at 3
• After 2 iterations: slow_pointer at 3, fast_pointer at 5
• After 3 iterations: slow_pointer at 4, fast_pointer at None (end of list)

Again, the slow_pointer is pointing to the middle element, which is 3. In this case, even though there’s another middle element 4, we consider the one closer to the beginning of the list.

Input/ Output