Python Program to Check if a Number is a Strong Number

This Python program checks if a number is a strong number or not. A strong number (also known as a strong factorial or a digital factorial) is a number that has a special property. The sum of the factorial of its digits is equal to the number itself.

A strong number is defined as a number whose sum of the factorials of its digits is equal to the original number itself. To determine if a number is a strong number, we break it down into its individual digits, calculate the factorial of each digit, and then sum up these factorials. If the resulting sum is equal to the original number, then it is considered a strong number.

Problem Statement

Write a Python program to determine whether a given number is a strong number or not. A strong number is a number that satisfies a specific property related to the factorial of its digits.

A number is considered a strong number if the sum of the factorials of its digits is equal to the number itself. To determine if a number is strong, you need to follow these steps:

1. Take a positive integer as input.
2. Extract each digit of the number.
3. Calculate the factorial of each digit.
4. Sum up the factorials of all the digits.
5. Compare the sum with the original number.
6. If the sum is equal to the original number, print that the number is a strong number. Otherwise, print that the number is not a strong number.

Write a Python function called is_strong_number(num) that takes an integer num as input and returns a boolean value indicating whether the number is a strong number or not.

Python Program to Check if a Number is a Strong Number

def factorial(n):
    if n == 0 or n == 1:
        return 1
    else:
        return n * factorial(n - 1)

def is_strong_number(num):
    temp = num
    sum_of_factorials = 0

    while temp > 0:
        digit = temp % 10
        sum_of_factorials += factorial(digit)
        temp //= 10

    return sum_of_factorials == num

# Test the function
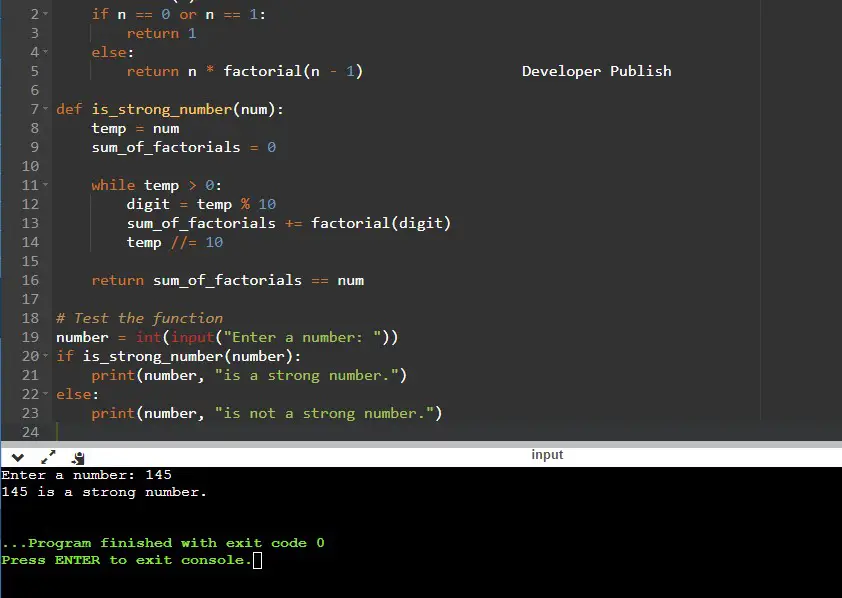
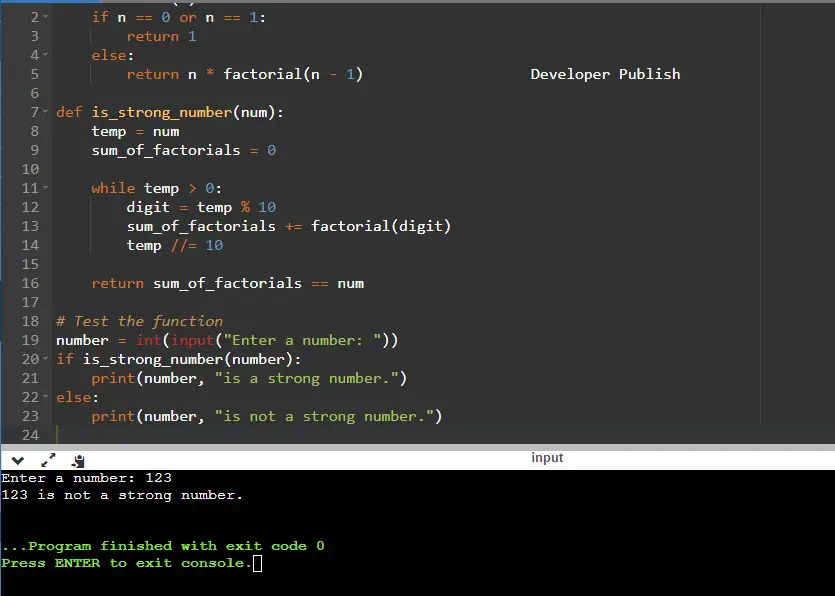
number = int(input("Enter a number: "))
if is_strong_number(number):
    print(number, "is a strong number.")
else:
    print(number, "is not a strong number.")

How it Work

The is_strong_number(num) function works as follows:

1. It takes an integer num as input, which represents the number we want to check for strongness.
2. The function initializes a variable temp with the value of num. This variable will be used for extracting the digits of the number.
3. It also initializes a variable sum_of_factorials to keep track of the sum of factorials of the digits.
4. A while loop is used to iterate until temp becomes 0. Within the loop:
   • The last digit of temp is obtained by performing temp % 10.
   • The factorial of the digit is calculated using the factorial() function.
   • The factorial is added to sum_of_factorials.
   • The value of temp is updated by dividing it by 10 (temp //= 10) to remove the last digit.
5. After the loop ends, the function compares sum_of_factorials with the original number num.
6. If sum_of_factorials is equal to num, the function returns True, indicating that the number is a strong number.
7. Otherwise, the function returns False, indicating that the number is not a strong number.

The factorial(n) function is a recursive function that calculates the factorial of a number n. It returns 1 if n is 0 or 1. Otherwise, it calculates n * factorial(n - 1) to obtain the factorial of n.

To test the is_strong_number(num) function, you can input different numbers and check if it correctly determines whether they are strong numbers or not. If the function returns True, it means the number is strong. If it returns False, it means the number is not strong.

Input/ Output