C Program to Solve the Magic Squares Puzzle

The Magic Squares puzzle is an intriguing mathematical problem that involves arranging numbers in a square grid such that the sum of each row, each column, and both diagonals is the same. In this puzzle, the goal is to determine whether a given square grid forms a valid magic square or not.

To solve this puzzle, we can develop a C program that prompts the user to enter the elements of the square grid, validates the input, and checks if the grid satisfies the conditions of a magic square. By performing the necessary calculations and comparisons, the program can provide the user with the solution.

Problem Statement

You are required to write a C program that solves the Magic Squares puzzle. A magic square is an arrangement of numbers in a square grid, where the numbers in each row, each column, and both diagonals have the same sum.

Your program should prompt the user to enter the elements of a square grid and determine whether it forms a valid magic square or not. The program should output either “Magic square found!” or “Not a magic square!” accordingly.

Your program should have the following specifications:

1. The size of the square grid should be 3×3.
2. The program should read the elements of the grid from the user.
3. The program should validate the input to ensure that valid integer values are entered for the elements.
4. The program should check if the input grid forms a valid magic square.
5. If the input grid is a valid magic square, the program should print “Magic square found!”.
6. If the input grid is not a valid magic square, the program should print “Not a magic square!”.

C Program to Solve the Magic Squares Puzzle

#include <stdio.h>
#include <stdbool.h>

#define SIZE 3 // Size of the square (3x3 in this example)

void solveMagicSquare(int magicSquare[SIZE][SIZE]) {
    int rowSum = 0, colSum = 0, diagSum1 = 0, diagSum2 = 0;

    // Calculate the sum of the first row
    for (int j = 0; j < SIZE; j++) {
        rowSum += magicSquare[0][j];
    }

    // Check if all rows, columns, and diagonals have the same sum
    for (int i = 0; i < SIZE; i++) {
        // Calculate the sum of the current row
        int currentRowSum = 0;
        for (int j = 0; j < SIZE; j++) {
            currentRowSum += magicSquare[i][j];
        }
        if (currentRowSum != rowSum) {
            printf("Not a magic square!\n");
            return;
        }

        // Calculate the sum of the current column
        int currentColSum = 0;
        for (int j = 0; j < SIZE; j++) {
            currentColSum += magicSquare[j][i];
        }
        if (currentColSum != rowSum) {
            printf("Not a magic square!\n");
            return;
        }

        // Calculate the sum of the main diagonal (top-left to bottom-right)
        diagSum1 += magicSquare[i][i];

        // Calculate the sum of the secondary diagonal (top-right to bottom-left)
        diagSum2 += magicSquare[i][SIZE - 1 - i];
    }

    if (diagSum1 != rowSum || diagSum2 != rowSum) {
        printf("Not a magic square!\n");
        return;
    }

    printf("Magic square found!\n");
}

int main() {
    int magicSquare[SIZE][SIZE];

    printf("Enter the elements of the magic square:\n");

    // Read the elements of the magic square
    for (int i = 0; i < SIZE; i++) {
        for (int j = 0; j < SIZE; j++) {
            scanf("%d", &magicSquare[i][j]);
        }
    }

    solveMagicSquare(magicSquare);

    return 0;
}

How it Works?

1. The program starts by defining the necessary libraries, including stdio.h for input/output operations and stdbool.h for using the bool data type.
2. A constant SIZE is defined to represent the size of the square grid. In this case, it is set to 3 since the puzzle specifies a 3×3 grid.
3. The program declares a function solveMagicSquare that takes a 2D array magicSquare as a parameter. This function will check if the input grid forms a valid magic square.
4. Inside the solveMagicSquare function, several variables are declared to keep track of the sums of rows, columns, and diagonals. rowSum is initialized to 0, and colSum, diagSum1, and diagSum2 are initially set to 0 as well.
5. A loop is used to calculate the sum of the first row by iterating over the columns of the grid.
6. Another loop is used to check if the sums of each row and column are equal to the sum of the first row. If any of the sums are different, the function prints “Not a magic square!” and returns.
7. Inside the same loop, the sums of the main diagonal (diagSum1) and the secondary diagonal (diagSum2) are calculated.
8. After the loop, a check is performed to verify if the sums of both diagonals are equal to the sum of the rows/columns. If not, the function prints “Not a magic square!” and returns.
9. If all the checks pass, the function prints “Magic square found!” indicating that the input grid is a valid magic square.
10. The main function is defined, where the program execution begins. It declares a 2D array magicSquare of size SIZE x SIZE to store the user’s input.
11. The program prompts the user to enter the elements of the magic square using nested loops that iterate over the rows and columns.
12. The input values are read using the scanf function and stored in the magicSquare array.
13. The solveMagicSquare function is called, passing the magicSquare array as an argument.
14. Finally, the program returns 0 to indicate successful execution.

This program takes user input for the elements of a 3×3 grid, checks if it forms a valid magic square, and provides the appropriate output.

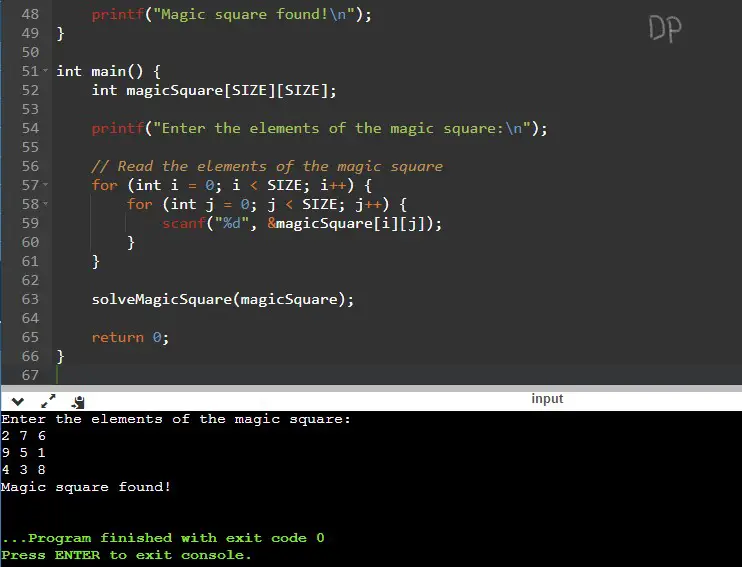
Input / Output

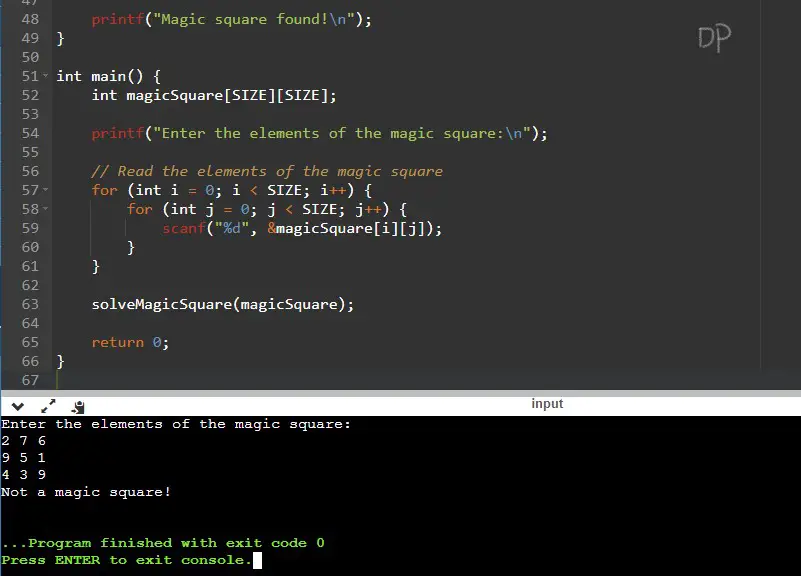
The input does not represent a magic square because the sum of the last row is 16, which is different from the expected sum of 15.