C# Program to Find Sum of Digits of a Number

Finding the sum of the digits of a number is a common problem in programming and mathematics. This task involves breaking down a given number into its individual digits and then adding them together. This concept is often used in various programming scenarios, including data validation, cryptography, and number manipulation.

Problem Statement

Write a C# program that takes an integer as input and calculates the sum of its digits.

C# Program to Find Sum of Digits of a Number

using System;

class Program
{
    static void Main()
    {
        Console.Write("Enter a number: ");
        int number = int.Parse(Console.ReadLine());

        int sumOfDigits = CalculateSumOfDigits(number);

        Console.WriteLine($"The sum of the digits of {number} is {sumOfDigits}");
    }

    static int CalculateSumOfDigits(int number)
    {
        int sum = 0;
        while (number > 0)
        {
            int digit = number % 10; // Get the last digit
            sum += digit;            // Add the digit to the sum
            number /= 10;            // Remove the last digit
        }
        return sum;
    }
}

How it Works

1. Input: We start with the number 12345.
2. Iteration:
   • In the first iteration, we use the modulo operator (%) to get the last digit: 12345 % 10 = 5. This digit is added to our running total (initialized to 0): sum = 0 + 5 = 5.
   • We then perform integer division by 10 to remove the last digit: 12345 / 10 = 1234. The number becomes 1234.
   • In the second iteration, we again use modulo to get the last digit: 1234 % 10 = 4. We add this digit to the sum: sum = 5 + 4 = 9.
   • We once more perform integer division by 10: 1234 / 10 = 123. The number becomes 123.
   • This process continues until there are no more digits left to process.
3. Termination Condition: We keep iterating and updating the sum until the number becomes zero (in integer division, or until we reach the end of the number in string form).
4. Output: When the number becomes zero, we have extracted and summed all the digits. The final value of sum is the sum of digits of the original number.

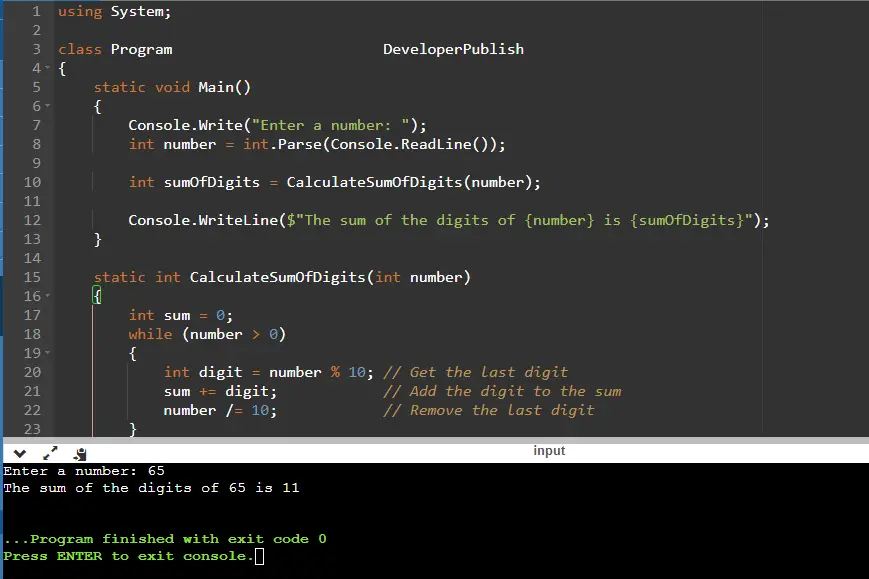
Input/ Output