Python Program to Perform Binary Search using Recursion

This Python program demonstrates the implementation of binary search using recursion. Binary search is an efficient algorithm to find a specific element in a sorted array by repeatedly dividing the search interval in half.

Problem Statement

Write a Python program that performs a binary search on a sorted array using recursion to find a target element. The program should return the index of the target element if found, otherwise return -1.

Python Program to Perform Binary Search using Recursion

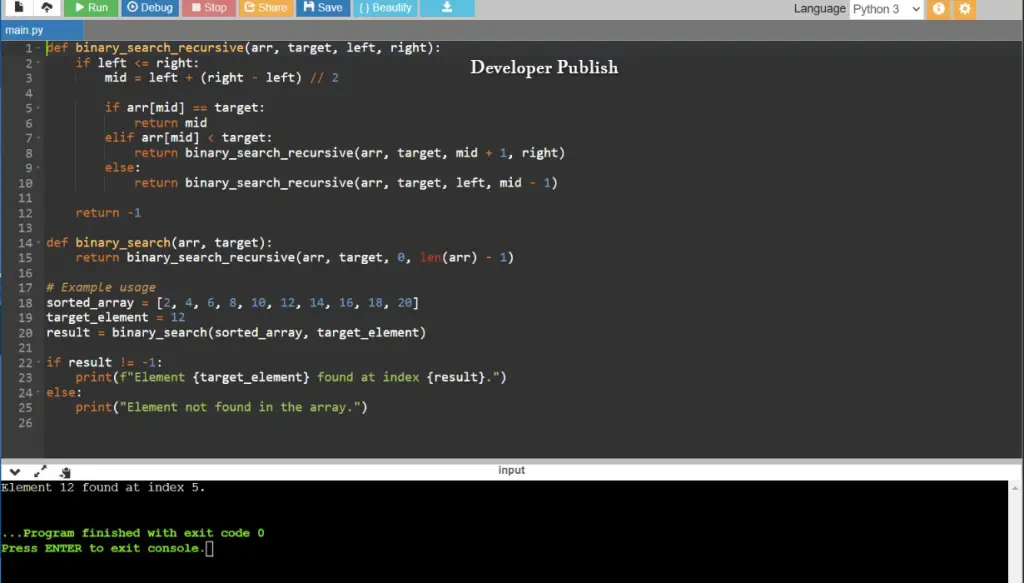
def binary_search_recursive(arr, target, left, right):
    if left <= right:
        mid = left + (right - left) // 2

        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            return binary_search_recursive(arr, target, mid + 1, right)
        else:
            return binary_search_recursive(arr, target, left, mid - 1)
    
    return -1

def binary_search(arr, target):
    return binary_search_recursive(arr, target, 0, len(arr) - 1)

# Example usage
sorted_array = [2, 4, 6, 8, 10, 12, 14, 16, 18, 20]
target_element = 12
result = binary_search(sorted_array, target_element)

if result != -1:
    print(f"Element {target_element} found at index {result}.")
else:
    print("Element not found in the array.")

How It Works

1. The binary_search_recursive function takes the sorted array arr, target element target, left and right indices of the search interval.
2. It calculates the middle index (mid) of the current search interval.
3. If the element at mid is equal to the target, the index mid is returned.
4. If the element at mid is less than the target, the function is called recursively on the right half of the array.
5. If the element at mid is greater than the target, the function is called recursively on the left half of the array.
6. The recursion stops when left is greater than right, indicating that the search interval has been exhausted.
7. The binary_search function initializes the search interval and calls the recursive function.

Input/Output