Python Program to Implement Merge Sort

Merge Sort is a popular sorting algorithm that follows the divide-and-conquer paradigm to efficiently sort an array or list of elements. It is known for its stability and consistent time complexity, making it suitable for sorting large datasets. The algorithm gets its name from the “merge” step, where it combines and arranges smaller sorted subarrays into a larger sorted array.

Problem Statement

You are given an unsorted list of integers. Your task is to implement the Merge Sort algorithm in python to sort the list in ascending order.

Python Program to Implement Merge Sort

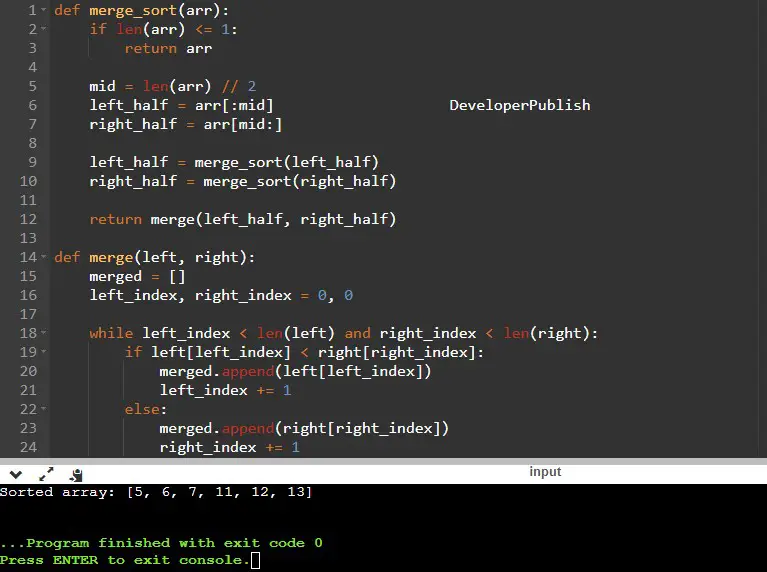
def merge_sort(arr):
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    left_half = arr[:mid]
    right_half = arr[mid:]

    left_half = merge_sort(left_half)
    right_half = merge_sort(right_half)

    return merge(left_half, right_half)

def merge(left, right):
    merged = []
    left_index, right_index = 0, 0

    while left_index < len(left) and right_index < len(right):
        if left[left_index] < right[right_index]:
            merged.append(left[left_index])
            left_index += 1
        else:
            merged.append(right[right_index])
            right_index += 1

    merged.extend(left[left_index:])
    merged.extend(right[right_index:])
    return merged

# Example usage
arr = [12, 11, 13, 5, 6, 7]
sorted_arr = merge_sort(arr)
print("Sorted array:", sorted_arr)

How it Works

1. Divide: The initial list is divided into smaller sublists recursively until each sublist contains only one element.
2. Conquer: Each one-element sublist is trivially sorted (base case).
3. Merge: The sorted sublists are merged back together in a sorted manner. The merging involves comparing elements from two sublists and placing them in the correct order.
4. Repeat: Steps 1 to 3 are repeated for larger sublists.cssCopy code[5, 12] | [8, 23] | [7, 19]
5. Merge Final: The final merge step combines the larger sublists to form the completely sorted list.

And that’s it! The list [12, 5, 23, 8, 19, 7] has been successfully sorted using the Merge Sort algorithm, resulting in the sorted list [5, 7, 8, 12, 19, 23].

The key insight of Merge Sort is to divide the problem into smaller subproblems, sort those subproblems, and then merge the sorted subproblems back together to obtain the overall sorted solution. This process guarantees that the entire list will be sorted correctly.

Input/ Output