Python Program to Implement D-ary Heap

This Python program implements a D-ary heap, which is a generalization of the binary heap where each parent node has up to D child nodes.

A D-ary heap is a data structure that generalizes the concept of a binary heap to allow each node to have D children, where D is a positive integer greater than or equal to 2. It’s a specialized tree-based data structure used primarily for efficient implementation of priority queues and heap-sort algorithms. D-ary heaps have properties similar to binary heaps, but they are more flexible and can be adapted for different use cases.

Problem Statement

You are tasked with implementing a D-ary heap data structure and performing specific operations on it in python.

Python Program to Implement D-ary Heap

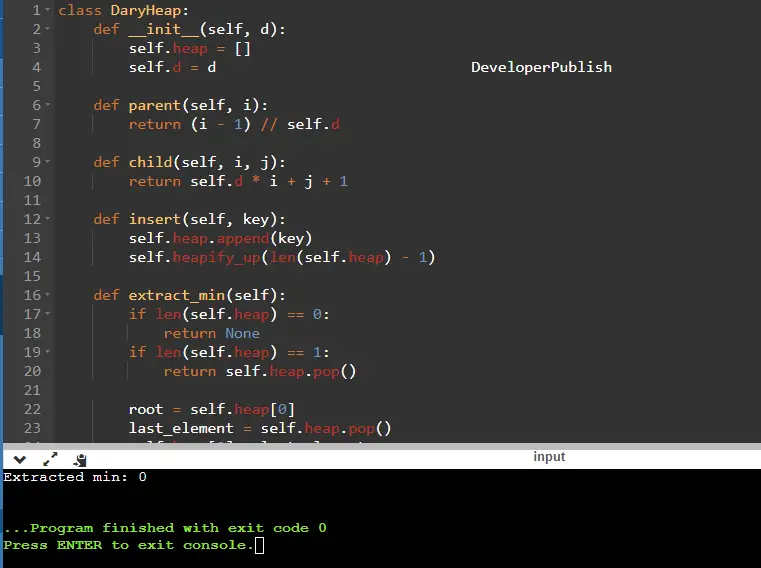
class DaryHeap:
    def __init__(self, d):
        self.heap = []
        self.d = d

    def parent(self, i):
        return (i - 1) // self.d

    def child(self, i, j):
        return self.d * i + j + 1

    def insert(self, key):
        self.heap.append(key)
        self.heapify_up(len(self.heap) - 1)

    def extract_min(self):
        if len(self.heap) == 0:
            return None
        if len(self.heap) == 1:
            return self.heap.pop()

        root = self.heap[0]
        last_element = self.heap.pop()
        self.heap[0] = last_element
        self.heapify_down(0)

        return root

    def heapify_up(self, i):
        while i > 0 and self.heap[i] < self.heap[self.parent(i)]:
            self.heap[i], self.heap[self.parent(i)] = self.heap[self.parent(i)], self.heap[i]
            i = self.parent(i)

    def heapify_down(self, i):
        min_child = self.min_child(i)
        while min_child is not None and self.heap[i] > self.heap[min_child]:
            self.heap[i], self.heap[min_child] = self.heap[min_child], self.heap[i]
            i = min_child
            min_child = self.min_child(i)

    def min_child(self, i):
        first_child = self.child(i, 0)
        if first_child >= len(self.heap):
            return None
        
        min_child = first_child
        for j in range(1, self.d):
            if first_child + j < len(self.heap) and self.heap[first_child + j] < self.heap[min_child]:
                min_child = first_child + j
        
        return min_child


# Example usage:
dary_heap = DaryHeap(3)
dary_heap.insert(3)
dary_heap.insert(2)
dary_heap.insert(1)
dary_heap.insert(7)
dary_heap.insert(0)
print("Extracted min:", dary_heap.extract_min())  # Extracted min: 0

How it Works

1. Structure:

• A D-ary heap is represented as a complete tree, meaning all levels of the tree are fully filled except possibly for the last level, which is filled from left to right.
• Each node in the heap has a value or key associated with it.

2. Insertion:

• To insert a new element into a D-ary heap, you start by adding it as a new leaf node at the end of the heap. This ensures that the tree remains complete.
• After insertion, you may need to perform a “heapify up” operation to maintain the heap property. In this operation, you compare the newly inserted element with its parent (which is at index (i-1)//D, where i is the index of the newly inserted element).
• If the heap property is violated (e.g., in a min-heap, the parent is larger than the child), you swap the child and the parent. You continue this process until the heap property is restored or until you reach the root of the heap.

3. Extraction (Min or Max):

• To extract the minimum (or maximum) element from a D-ary heap, you typically remove the root node (which holds the minimum or maximum value) and replace it with the last leaf node in the heap.
• After this replacement, you may need to perform a “heapify down” operation to maintain the heap property. In this operation, you compare the new root node with its children (which are at indices D*i + 1, D*i + 2, …, D*i + D, where i is the index of the root).
• You find the child with the smallest (for a min-heap) or largest (for a max-heap) value and swap the root with that child if the heap property is violated. You continue this process recursively down the tree until the heap property is restored or until you reach a leaf node.

4. Time Complexity:

• The time complexity of insertion and extraction operations in a D-ary heap is O(log_D(N)), where N is the number of nodes in the heap. This is because you traverse the height of the tree, and each level has D children.

5. Use Cases:

• D-ary heaps are commonly used to implement efficient priority queues in algorithms like Dijkstra’s shortest path algorithm and Prim’s minimum spanning tree algorithm.
• They are also used in certain specialized sorting algorithms like D-ary heap sort.

Input/ Output