Python Program to Implement Counting Sort

Counting Sort is a non-comparative sorting algorithm that works particularly well when the range of input values is known and relatively small. It’s efficient because it doesn’t rely on comparisons between elements, unlike algorithms like Quick Sort or Merge Sort. Instead, it directly uses the input values themselves to determine their sorted positions. Counting Sort’s time complexity is O(n + k), where n is the number of elements in the input array and k is the range of input values.

Problem Statement

You are given an array of integers. Implement the Counting Sort algorithm in Python to sort the array in non-decreasing order.

Python Program to Implement Counting Sort

def counting_sort(arr):
    # Find the range of elements in the array
    max_value = max(arr)
    min_value = min(arr)
    range_of_elements = max_value - min_value + 1

    # Initialize a count array to store the frequency of elements
    count_array = [0] * range_of_elements

    # Count the frequency of each element in the input array
    for num in arr:
        count_array[num - min_value] += 1

    # Update the count array to store the cumulative count
    for i in range(1, len(count_array)):
        count_array[i] += count_array[i - 1]

    # Create the output array
    output_array = [0] * len(arr)
    
    # Build the output array using the count array
    for num in reversed(arr):
        output_array[count_array[num - min_value] - 1] = num
        count_array[num - min_value] -= 1

    return output_array

# Example usage
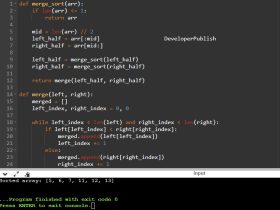
input_array = [4, 2, 2, 8, 3, 3, 1]
sorted_array = counting_sort(input_array)
print("Input Array:", input_array)
print("Sorted Array:", sorted_array)

How it Works

Step 1: Finding the Range

• Find the maximum and minimum values in the input array to determine the range of values. In this case, the maximum value is 8 and the minimum value is 1, so the range is [1, 8].

Step 2: Create a Count Array

• Create a count array to store the frequency of each value within the specified range [1, 8]. Initialize all elements of the count array to zero.

Step 3: Count Frequencies

• Count the occurrences of each value in the input array and update the count array accordingl

Step 4: Calculate Cumulative Counts

• Modify the count array to store cumulative counts. This step helps determine the positions of the elements in the sorted array.

mathematically.

Step 5: Build the Sorted Array

• Create a new array to store the sorted output. Traverse the input array in reverse order, and for each element, find its position in the sorted array using the cumulative count array. Decrease the cumulative count for that element’s value by one.

Input/ Output