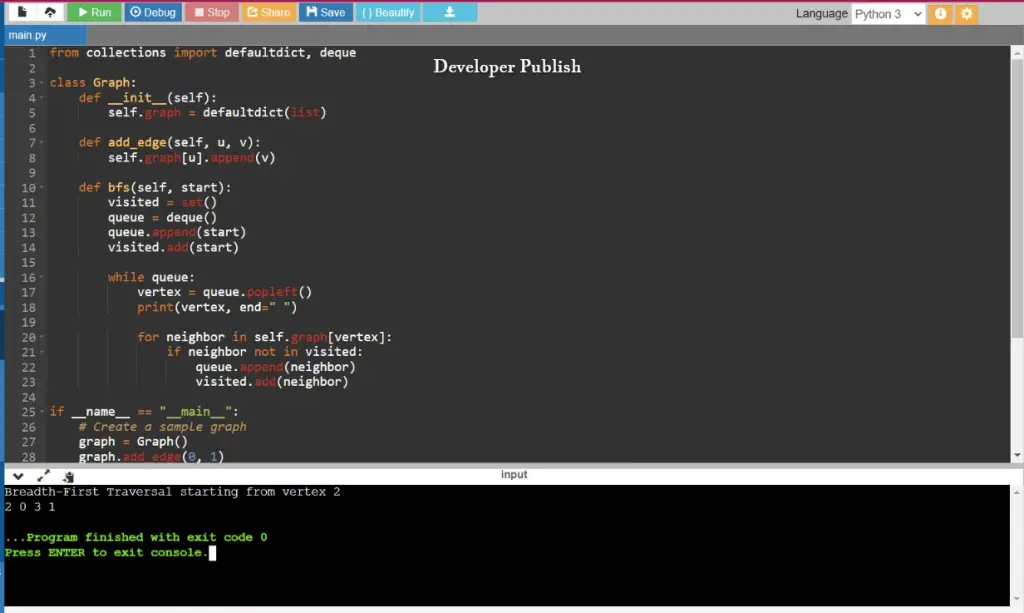
Python Program to Implement Breadth-First Search on a Graph

This Python program implements Breadth-First Search (BFS) on a graph using a queue. BFS is used to traverse or search a graph by visiting all the vertices and edges in breadth-first order, starting from a specified source node.

Breadth-First Search (BFS) is a fundamental graph traversal algorithm that explores all the vertices of a graph in breadth-first order, i.e., it visits all the neighbors of a vertex before moving to their neighbors. BFS is often used to find the shortest path in an unweighted graph and can be employed in various graph-related problems.

Problem Statement

Given a graph represented as an adjacency list, implement the Breadth-First Search (BFS) algorithm to traverse the graph starting from a specified source vertex and print the order in which vertices are visited.

Python Program to Implement Breadth-First Search on a Graph

from collections import defaultdict, deque

class Graph:
    def __init__(self):
        self.graph = defaultdict(list)

    def add_edge(self, u, v):
        self.graph[u].append(v)

    def bfs(self, start):
        visited = set()
        queue = deque()
        queue.append(start)
        visited.add(start)

        while queue:
            vertex = queue.popleft()
            print(vertex, end=" ")

            for neighbor in self.graph[vertex]:
                if neighbor not in visited:
                    queue.append(neighbor)
                    visited.add(neighbor)

if __name__ == "__main__":
    # Create a sample graph
    graph = Graph()
    graph.add_edge(0, 1)
    graph.add_edge(0, 2)
    graph.add_edge(1, 2)
    graph.add_edge(2, 0)
    graph.add_edge(2, 3)
    graph.add_edge(3, 3)

    start_vertex = 2  # Specify the starting vertex

    print("Breadth-First Traversal starting from vertex", start_vertex)
    graph.bfs(start_vertex)

How It Works

1. We create a Graph class to represent the graph using an adjacency list.
2. The add_edge method is used to add edges to the graph.
3. The bfs method performs the BFS traversal. It uses a queue to keep track of vertices to visit and a set to mark visited vertices.
4. We start BFS from the specified start_vertex, enqueue it, and mark it as visited.
5. While the queue is not empty, we dequeue a vertex, print it, and enqueue its unvisited neighbors.
6. The process continues until all reachable vertices are visited.

Input/Output