In this implementation, each node of the binary tree is represented using an object, and these objects are linked together to form the structure of the tree. Each node contains a value and references (pointers) to its left child and right child nodes. If a child node is absent, the corresponding reference is set to None.
Problem Statement
You are given a list of integers representing the values that need to be inserted into a binary tree using python. Your task is to implement a binary tree using linked list-based nodes and perform an in order traversal of the tree.
Python Program to Implement Binary Tree using Linked List
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinaryTree:
def __init__(self, root_value):
self.root = TreeNode(root_value)
def insert(self, value):
self._insert_recursive(self.root, value)
def _insert_recursive(self, current_node, value):
if value <= current_node.value:
if current_node.left is None:
current_node.left = TreeNode(value)
else:
self._insert_recursive(current_node.left, value)
else:
if current_node.right is None:
current_node.right = TreeNode(value)
else:
self._insert_recursive(current_node.right, value)
def search(self, value):
return self._search_recursive(self.root, value)
def _search_recursive(self, current_node, value):
if current_node is None:
return False
if current_node.value == value:
return True
elif value < current_node.value:
return self._search_recursive(current_node.left, value)
else:
return self._search_recursive(current_node.right, value)
def inorder_traversal(self):
result = []
self._inorder_traversal_recursive(self.root, result)
return result
def _inorder_traversal_recursive(self, current_node, result):
if current_node is not None:
self._inorder_traversal_recursive(current_node.left, result)
result.append(current_node.value)
self._inorder_traversal_recursive(current_node.right, result)
# Example usage
tree = BinaryTree(10)
tree.insert(5)
tree.insert(15)
tree.insert(3)
tree.insert(7)
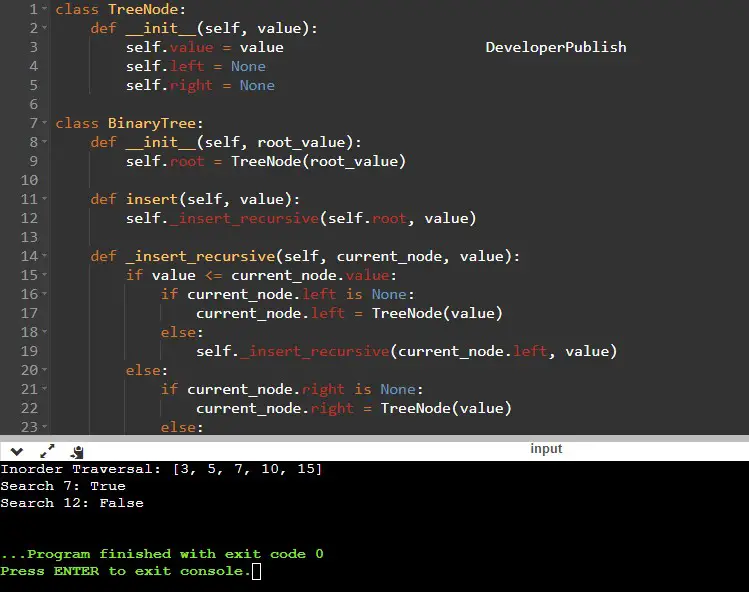
print("Inorder Traversal:", tree.inorder_traversal())
print("Search 7:", tree.search(7))
print("Search 12:", tree.search(12))
How it Works
Step 1: Define the TreeNode Class The TreeNode class is defined to represent the nodes of the binary tree. Each node contains three attributes: value to store the value of the node, left to point to the left child node, and right to point to the right child node.
Step 2: Define the BinaryTree Class The BinaryTree class is defined with an __init__ method that takes the root value as an argument. It initializes the root node using the provided value.
The insert method is used to insert values into the binary tree. It starts from the root and traverses the tree to find the appropriate position for the new value. If the value is less than the current node’s value, it goes to the left child; otherwise, it goes to the right child. If the child node is empty, a new node is created and assigned to the corresponding child.
The inorder_traversal method performs an inorder traversal of the binary tree. It starts from the root and recursively traverses the left subtree, visits the current node, and then recursively traverses the right subtree. The values encountered during this traversal are added to the result list.
Step 3: Example Usage
Step 4: Output
Input/ Output
