C++ Program to Find Roots of Quadratic Equation

In this post, you’ll learn how to Find Roots of Quadratic Equation in C++ programming language.

In this tutorial, you will learn how to find the Roots of Quadratic Equation, with the comparison operator, equal-to operator, mathematical operations and the decision making statements using the C++ language. Let’s look at the below source code.

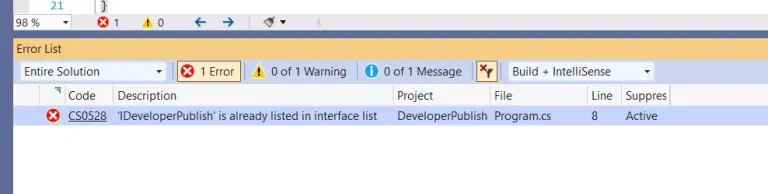
How to Find Roots of Quadratic Equation?

Source Code

#include <iostream>
#include <cmath>
using namespace std;
int main() 
{
    float a, b, c, x1, x2, discriminant, realPart, imaginaryPart;
    cin >> a >> b >> c;
    cout << "Enter coefficients a, b and c: "<< a <<", "<< b <<", "<< c <<endl;
    discriminant = b*b - 4*a*c;
    if (discriminant > 0) 
      {
        x1 = (-b + sqrt(discriminant)) / (2*a);
        x2 = (-b - sqrt(discriminant)) / (2*a);
        cout << "\nRoots are real and different." << endl;
        cout << "x1 = " << x1 << endl;
        cout << "x2 = " << x2 << endl;
      }
    else if (discriminant == 0)
      {
        cout << "\nRoots are real and same." << endl;
        x1 = -b/(2*a);
        cout << "x1 = x2 =" << x1 << endl;
      }
    else 
      {
        realPart = -b/(2*a);
        imaginaryPart =sqrt(-discriminant)/(2*a);
        cout << "\nRoots are complex and different."  << endl;
        cout << "x1 = " << realPart << "+" << imaginaryPart << "i" << endl;
        cout << "x2 = " << realPart << "-" << imaginaryPart << "i" << endl;
      }
    return 0;
}

Input

1 -2 1

Output

Enter coefficients a, b and c: 1, -2, 1
Roots are real and same.
x1 = x2 =1

#include <iostream>, #include<cmath>

• This line which is called the header file. #include statement tells the compiler to use available files and <iostream>is the name of the specific that we have used in this code. The <iostream> file stands for Input and Output statement.
• The <cmath> file declares a set of functions to perform mathematical operations.

using namespace std;

• The C++ has a standard library that has files for different functions and this line is used to access the standard file for input and output statements.

int main();

• This line usually controls the function of the code, as it calls the functions to perform their tasks.
• The int main()shows that the input value is a type of integer, once the program is executed the function returns to the main function, by using the statement ‘return 0;’.

{ }

• The opening ‘ { ‘ and the closing ‘ } ‘ curly braces mark the start and the finish of the main function
• Every statement and value between these braces belong to the main function.

The above statements are the main factors that support the function of the source code. Now we can look into the working and layout of the code’s function.

A Quadratic equation is of the form ax²+bx+c = 0 (where a, b and c are coefficients), and to find it’s roots we use the formula given below.

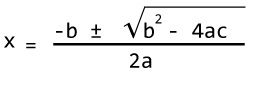
The term b² – 4ac is known as the discriminant of a quadratic equation. The discriminant tells the nature of the roots.

• If discriminant is greater than 0, the roots are real and different.
• If discriminant is equal to 0, the roots are real and equal.
• If discriminant is less than 0, the roots are complex and different.

Based on the above conditions we can have created a source code to find the roots of the quadratic equation, by using the comparison operator, equal-to operator, mathematical operations and the decision making statements.

1. First we declare the variables (a, b, c, x1, x2, discriminant, realPart, imaginaryPart) as float values.
2. Next, we obtain the values of the discriminant from the user and store them a, b, c using the cin >> and cout << to display them.
3. The formula to find the discriminant is discriminant = b*b - 4*a*c (b² – 4ac).
4. To find the roots according to the discriminant value, we must use the following formulas in the source code.

1. Using the decision making statements we assign the conditions to be satisfied – if (discriminant > 0) else if (discriminant == 0), and if the condition is satisfied, the operation under it in {} will be performed.
2. If both these conditions are not satisfied the next else statement is executed.
3. if (discriminant > 0) – this statement’s formula, as in the above image is written as x1 = (-b + sqrt(discriminant)) / (2*a);  and x2 = (-b - sqrt(discriminant)) / (2*a); .In this the sqrt function is used to find the square root of a number.
4. else if (discriminant == 0) – this statement’s formula as in the above image is written as x1 = -b/(2*a);
5. And for the last condition if determinant<0, the formula as in the above image is written as realPart = -b/(2*a); and imaginaryPart =sqrt(-discriminant)/(2*a); . The realPart and the imaginaryPart are just variables which holds the answer after the function is executed.
6. When you look at the last output statement, is should be displayed as x1 = -0.5+0.866025iand x2 = -0.5-0.866025i and hence the statement cout << "x1 = " << realPart << "+" << imaginaryPart << "i" << endl;

Note: The ‘ << endl ‘ in the code is used to end the current line and move to the next line and ‘\n’ is also a new line function, to understand how both the functions work exclude it from the code, move it around and work with it.